题目内容
若定义在 上的函数
上的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 ,使得
,使得 对于任意的实数
对于任意的实数 都成立,则称
都成立,则称 是一个“
是一个“ 的相关函数”,则下列结论正确的是 ( )
的相关函数”,则下列结论正确的是 ( )
A. 是常数函数中唯一一个“
是常数函数中唯一一个“ 的相关函数”;
的相关函数”;
B. 是一个“
是一个“ 的相关函数”;
的相关函数”;
C. 是一个“
是一个“ 的相关函数”;
的相关函数”;
D.“ 的相关函数”至少有一个零点
的相关函数”至少有一个零点
D
【解析】
试题分析:对于A,设f(x)=C是一个“ 的相关函数”,则
的相关函数”,则 ,当
,当 时,可以取遍实数集,因此f(x)=0不是唯一一个常值“
时,可以取遍实数集,因此f(x)=0不是唯一一个常值“ ﹣伴随函数”,故A不正确;
﹣伴随函数”,故A不正确;
对于B,用反证法,假设 是一个“
是一个“ 的相关函数”,所以
的相关函数”,所以 ,即
,即 对任意实数x成立,所以
对任意实数x成立,所以 无解,所以
无解,所以 不是一个“
不是一个“ 的相关函数”,故B不正确;
的相关函数”,故B不正确;
对于C,假设 是一个“
是一个“ 的相关函数”,则
的相关函数”,则 对任意实数
对任意实数 成立,则
成立,则 ,此式有解,
,此式有解, 是一个“
是一个“ 的相关函数”,故C不正确;
的相关函数”,故C不正确;
对于D,令x=0,得 ,所以
,所以 ,
,
若f(0)=0,显然f(x)=0有实数根;若 ,
, .
.
又因为f(x)的函数图象是连续不断,所以f(x)在 上必有实数根.因此任意的“
上必有实数根.因此任意的“ 的相关函数”必有根,即任意“
的相关函数”必有根,即任意“ 的相关函数”至少有一个零点,
的相关函数”至少有一个零点,
故D正确.
考点:命题的真假判断与应用.菁优

练习册系列答案
相关题目
 ”是“
”是“ ”的充分不必要条件,则
”的充分不必要条件,则 的取值范围为 。
的取值范围为 。 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, ,那么在区间
,那么在区间 内,关于
内,关于 的方程
的方程 (
( 且
且 )有
)有 个不同的根,则
个不同的根,则 的取值范围是 .
的取值范围是 .  .
. ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围; 时,有
时,有 .若对于任意的实数
.若对于任意的实数 ,存在最大的实数
,存在最大的实数 ,使得当
,使得当 时,
时, 恒成立,试求用
恒成立,试求用 表示
表示 的表达式.
的表达式. 年的前
年的前 个月内对某种商品的需求总量
个月内对某种商品的需求总量 (万件)与月份
(万件)与月份 的近似关系式是
的近似关系式是 ,则
,则 年的第
年的第 月的需求量
月的需求量 (万件)与月份
(万件)与月份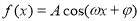 (
(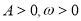 )的图象如右图所示,为了得到
)的图象如右图所示,为了得到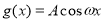 的图象,可以将
的图象,可以将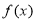 的图象( )
的图象( ) 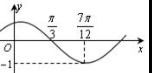
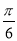 个单位长度
个单位长度 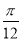 个单位长度
个单位长度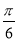 个单位长度
个单位长度  个单位长度
个单位长度 的三内角
的三内角 与所对的边
与所对的边 满足
满足 。
。 的大小;
的大小; 为长度的线段能围成以
为长度的线段能围成以 为斜边的直角三角形,试求实数
为斜边的直角三角形,试求实数 的取值范围.
的取值范围. ”为真命题,则“
”为真命题,则“ ”为真命题
”为真命题  ”为假命题,则“
”为假命题,则“ ”为真命题
”为真命题  ”的否命题为真命题
”的否命题为真命题 ,则方程
,则方程 有实根”的逆命题为真命题
有实根”的逆命题为真命题 ,有下列4个结论:
,有下列4个结论: ,都有
,都有 恒成立;
恒成立;
 ,对于一切
,对于一切 恒成立;
恒成立; 有
有 个零点;
个零点; ,不等式
,不等式 恒成立.
恒成立.