题目内容
已知 的三内角
的三内角 与所对的边
与所对的边 满足
满足 。
。
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)如果用 为长度的线段能围成以
为长度的线段能围成以 为斜边的直角三角形,试求实数
为斜边的直角三角形,试求实数 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】
试题分析:(Ⅰ)根据正弦定理与两角和的正弦公式化简题中等式,可得2sinBcosA=sin(A+C),再根据诱导公式与三角形内角的正弦大于零,解出cosA= ,,从而可得角
,,从而可得角
(Ⅱ)根据题意利用勾股定理,得到 ,利用三角恒等变换公式化简整理,得到
,利用三角恒等变换公式化简整理,得到
 ,最后根据
,最后根据 ),利用正弦函数的图象与性质加以计算,得到
),利用正弦函数的图象与性质加以计算,得到 ,由此即可算出实数p的取值范围.
,由此即可算出实数p的取值范围.
试题解析:【解析】
(Ⅰ)∵ 中
中 ,∴根据正弦定理,得
,∴根据正弦定理,得
即cosA(2sinB-sinC)=sinAcosC,化简得2sinBcosA=sinAcosC+cosAsinC=sin(A+C),
∵在 中,sin(A+C)=sin(π-B)=sinB>0,∴2sinBcosA=sinB,可得cosA=
中,sin(A+C)=sin(π-B)=sinB>0,∴2sinBcosA=sinB,可得cosA= ,
,

(Ⅱ)∵用psinA,sinB,sinC为长度的线段能围成以psinA为斜边的直角三角形,∴ ,
,



 ,
,
因此,实数p的取值范围是 .
.
考点:三角形中的几何计算;正弦定理.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 的焦点坐标为( )
的焦点坐标为( ) B.
B. C.
C. D.
D.
 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 ,使得
,使得 对于任意的实数
对于任意的实数 都成立,则称
都成立,则称 是一个“
是一个“ 的相关函数”,则下列结论正确的是 ( )
的相关函数”,则下列结论正确的是 ( ) 是常数函数中唯一一个“
是常数函数中唯一一个“ 的相关函数”;
的相关函数”; 是一个“
是一个“ 的相关函数”;
的相关函数”; 是一个“
是一个“ 的相关函数”至少有一个零点
的相关函数”至少有一个零点 前
前 项的积为
项的积为 ,且公比
,且公比 ,若
,若 ,则( )
,则( ) B.
B. C.
C. D.
D.
 满足
满足 ,且
,且 ,则该数列的通项公式
,则该数列的通项公式 = .
= . 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,则
,则 B.
B. C.
C. D.
D.
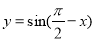 的图象 ( )
的图象 ( )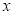 轴对称 (B)关于
轴对称 (B)关于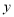 轴对称
轴对称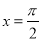 对称
对称