题目内容
四个条件:b>0>a;0>a>b;a>0>b;a>b>0中,能使 成立的充分条件的个数是
成立的充分条件的个数是
- A.1
- B.2
- C.3
- D.4
C
分析:利用不等式的基本性质,分别进行变形,可以得到 ,即为使
,即为使 成立的充分条件.
成立的充分条件.
解答:由题意,b>0>a时, ,∴
,∴ ;
;
0>a>b时, ,∴
,∴ ;
;
a>0>b时, ,∴
,∴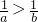 ;
;
a>b>0时, ,∴
,∴
从而能使 成立的充分条件的个数是3个
成立的充分条件的个数是3个
故选C.
点评:本题以不等式为载体,考查充分条件,解题的关键利用不等式的基本性质,分别进行变形.
分析:利用不等式的基本性质,分别进行变形,可以得到
 ,即为使
,即为使 成立的充分条件.
成立的充分条件.解答:由题意,b>0>a时,
 ,∴
,∴ ;
;0>a>b时,
 ,∴
,∴ ;
;a>0>b时,
 ,∴
,∴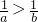 ;
;a>b>0时,
 ,∴
,∴
从而能使
 成立的充分条件的个数是3个
成立的充分条件的个数是3个故选C.
点评:本题以不等式为载体,考查充分条件,解题的关键利用不等式的基本性质,分别进行变形.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
给出四个条件:①b>0>a;②0>a>b;③a>0>b;④a>b>0,其中能使
<
成立的条件是( )
| 1 |
| a |
| 1 |
| b |
| A、②③④ | B、①③④ |
| C、①②④ | D、①②③④ |