题目内容
16.函数f(x)=|x-1|+|x+m|(m>0).(1)若m=2,求f(x)≤3的解集;
(2)若f(x)≤3对任意x∈[-2,-m]恒成立,求m的取值范围.
分析 (1)m=2时得到,$f(x)=\left\{\begin{array}{l}{-2x-1}&{x<-2}\\{3}&{-2≤x≤1}\\{2x+1}&{x>1}\end{array}\right.$,求出每段上函数f(x)的范围,这样便能得出f(x)≤3的解;
(2)先根据x的范围,可去绝对值号得到f(x)=-2x+1-m,从而看出该函数在[-2,-m]上单调递减,从而f(-2)=5-m是f(x)的最大值,这样根据条件即可得到5-m≤3,这样便可得出m的取值范围.
解答 解:(1)m=2时,f(x)=|x-1|+|x+2|=$\left\{\begin{array}{l}{-2x-1}&{x<-2}\\{3}&{-2≤x≤1}\\{2x+1}&{x>1}\end{array}\right.$;
∴①x<-2时,f(x)=-2x-1>f(-2)=3;
②-2≤x≤1时,f(x)=3;
③x>1时,f(x)=2x+1>3;
∴f(x)≤3的解集为[-2,1];
(2)x∈[-2,-m];
∴f(x)=-2x+1-m,该函数在[-2,-m]上单调递减;
∴f(x)≤f(-2)=5-m;
∵f(x)≤3对于任意x∈[-2,-m]恒成立;
∴5-m≤3;
∴m≥2;
∴m的取值范围为[2,+∞).
点评 考查含绝对值函数的处理方法:去绝对值号,分段函数值域的求法,以及一次函数的单调性,根据单调性求函数最值.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
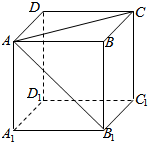 在如图所示的正方体ABCD-A1B1C1D1中,求:
在如图所示的正方体ABCD-A1B1C1D1中,求: