题目内容
在平面直角坐标系中,以坐标原点为极点,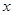 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线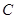 的极坐标方程为
的极坐标方程为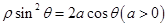 ,过点
,过点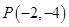 的直线
的直线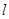 的参数方程为
的参数方程为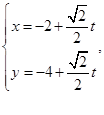 (
(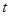 为参数),直线
为参数),直线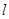 与曲线
与曲线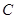 相交于
相交于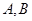 两点.
两点.
(1)写出曲线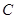 的直角坐标方程和直线
的直角坐标方程和直线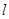 的普通方程;
的普通方程;
(2)若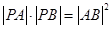 ,求
,求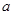 的值.
的值.
(1)直角坐标方程为 ,普通方程为
,普通方程为 ;(2)
;(2) .
.
解析试题分析:(1)由 得
得 ,极坐标方程
,极坐标方程 得
得 ,将参数方程中的参数
,将参数方程中的参数 消去可得
消去可得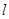 的普通方程;(2)将参数方程代入直角坐标方程化为关于
的普通方程;(2)将参数方程代入直角坐标方程化为关于 的一元二次方程,结合条件利用韦达定理解出
的一元二次方程,结合条件利用韦达定理解出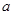 .
.
试题解析:(1)由 得
得
∴曲线 的直角坐标方程为
的直角坐标方程为
直线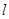 的普通方程为
的普通方程为
(2)将直线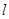 的参数方程代入曲线
的参数方程代入曲线 的直角坐标方程
的直角坐标方程 中,
中,
得
设 两点对应的参数分别为
两点对应的参数分别为
则有
∵
∴ 即
即
∴
解之得: 或
或 (舍去)
(舍去)
∴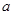 的值为
的值为 .
.
考点:1.参数方程;2.极坐标方程;3.一元二次方程的解法.

练习册系列答案
相关题目
 (
( 为参数)相交于
为参数)相交于 、
、 两点,则|
两点,则| |= .
|= .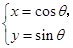 (
(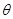 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).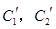 .写出
.写出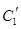 与
与 公共点的个数和C
公共点的个数和C 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由. 中,已知直线
中,已知直线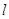 的参数方程
的参数方程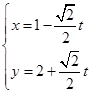 (
(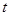 为参数),直线
为参数),直线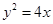 相交于
相交于 两点,求线段
两点,求线段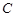 的参数方程为
的参数方程为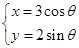 (
(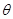 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换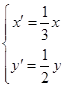 得到曲线
得到曲线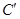 .
. 在曲线
在曲线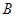
 ,当点
,当点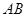 中点
中点 的轨迹方程.
的轨迹方程.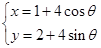 (
( 为参数),直线
为参数),直线 经过定点P(3,5),倾斜角为
经过定点P(3,5),倾斜角为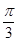 (1)写出直线
(1)写出直线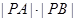 的值
的值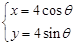 (
(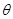 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角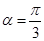 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;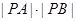 的值。
的值。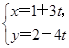 (t为参数)与直线l2:2x-4y=5相交于点B,又点A(1,2),求|AB|.
(t为参数)与直线l2:2x-4y=5相交于点B,又点A(1,2),求|AB|.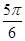 .
.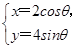 (θ为参数)交于A,B两点,求|PA|·|PB|.
(θ为参数)交于A,B两点,求|PA|·|PB|.