题目内容
已知曲线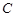 的参数方程为
的参数方程为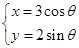 (
(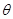 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换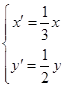 得到曲线
得到曲线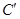 .
.
(1)求曲线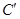 的普通方程;
的普通方程;
(2)若点 在曲线
在曲线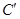 上,点
上,点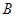
 ,当点
,当点 在曲线
在曲线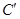 上运动时,求
上运动时,求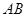 中点
中点 的轨迹方程.
的轨迹方程.
(1) ;(2)
;(2) .
.
解析试题分析:本题主要考查参数方程与普通方程的互化、中点坐标公式等基础知识,考查学生的转化能力、分析能力、计算能力.第一问,将曲线C的坐标直接代入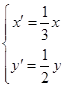 中,得到曲线
中,得到曲线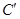 的参数方程,再利用参数方程与普通方程的互化公式,将其转化为普通方程;第二问,设出P、A点坐标,利用中点坐标公式,得出
的参数方程,再利用参数方程与普通方程的互化公式,将其转化为普通方程;第二问,设出P、A点坐标,利用中点坐标公式,得出 ,由于点A在曲线
,由于点A在曲线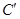 上,所以将得到的
上,所以将得到的 代入到曲线
代入到曲线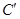 中,得到
中,得到 的关系,即为
的关系,即为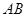 中点
中点 的轨迹方程.
的轨迹方程.
试题解析:(1)将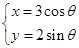 代入
代入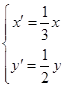 ,得
,得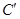 的参数方程为
的参数方程为
∴曲线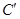 的普通方程为
的普通方程为 . 5分
. 5分
(2)设 ,
, ,又
,又 ,且
,且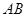 中点为
中点为
所以有:
又点 在曲线
在曲线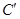 上,∴代入
上,∴代入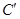 的普通方程
的普通方程 得
得
∴动点 的轨迹方程为
的轨迹方程为 . 10分
. 10分
考点:参数方程与普通方程的互化、中点坐标公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为极点,直线过圆
为极点,直线过圆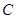 :
: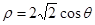 的圆心
的圆心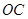 垂直,则直线的极坐标方程为 .
垂直,则直线的极坐标方程为 . (
( 为参数)与曲线
为参数)与曲线 (
( 为参数)的交点个数为____________.
为参数)的交点个数为____________.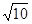 ,0)作直线l,交曲线
,0)作直线l,交曲线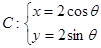 (θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.
(θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.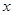 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线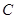 的极坐标方程为
的极坐标方程为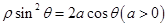 ,过点
,过点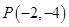 的直线
的直线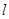 的参数方程为
的参数方程为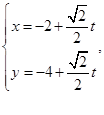 (
(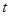 为参数),直线
为参数),直线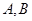 两点.
两点.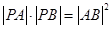 ,求
,求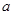 的值.
的值.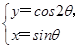 化为普通方程,并说明它表示的图形.
化为普通方程,并说明它表示的图形. 倍.
倍.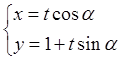 (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.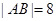 ,求α的值.
,求α的值.