题目内容
 如图,在直角坐标系xOy中,过点P(2,0)的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
如图,在直角坐标系xOy中,过点P(2,0)的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.(1)求x1x2与y1 y2的值;
(2)以线段MN为直径作圆H(H为圆心),证明抛物线的顶点在圆H的圆周上.
分析:(1)先设出直线方程,联立抛物线方程消去x可得y2-2my-4=0,再根据点M,N的纵坐标y1与y2是上述方程的根,可求出
y1 y2的值;最后根据M(x1,y1),N(x2,y2)两点是抛物线上的点代入再结合上面求的结论即可求出求x1x2的值;
(2)设直线OM,ON斜率分别为k1,k2,求出k1•k2=
=
=-1即可证明结论.
y1 y2的值;最后根据M(x1,y1),N(x2,y2)两点是抛物线上的点代入再结合上面求的结论即可求出求x1x2的值;
(2)设直线OM,ON斜率分别为k1,k2,求出k1•k2=
| y1•y2 |
| x1•x2 |
| -4 |
| 4 |
解答:解:(1)因为直线l不可能是X轴,所以设l的方程为x=my+2,
将其代入y2=2x,消去x可得y2-2my-4=0,
点M,N的纵坐标y1与y2是上述方程的根,故y1•y2=-4.
由y12=2x1,y22=2x2,相乘得(y1y2)2=4x1x2,
所以x1•x2=
=4.
(2)证明:直线OM,ON斜率分别为k1,k2,
则k1=
,k2=
.
因此k1•k2=
=
=-1.
所以OM⊥ON.
所以抛物线的顶点O在圆H的圆周上.
将其代入y2=2x,消去x可得y2-2my-4=0,
点M,N的纵坐标y1与y2是上述方程的根,故y1•y2=-4.
由y12=2x1,y22=2x2,相乘得(y1y2)2=4x1x2,
所以x1•x2=
| (y1y2)2 |
| 4 |
(2)证明:直线OM,ON斜率分别为k1,k2,
则k1=
| y1 |
| x1 |
| y2 |
| x2 |
因此k1•k2=
| y1•y2 |
| x1•x2 |
| -4 |
| 4 |
所以OM⊥ON.
所以抛物线的顶点O在圆H的圆周上.
点评:本题主要考查直线与抛物线的综合问题以及直线与圆的综合问题.考查考学分析问题和解决问题的能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.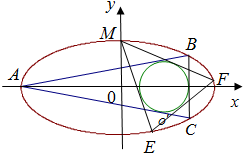 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且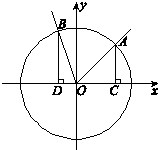 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: