题目内容
8. 有一块半径为R(R为正常数)的半圆形空地,开发商计划征地建一个游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在半圆周上,如图.
有一块半径为R(R为正常数)的半圆形空地,开发商计划征地建一个游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在半圆周上,如图.(1)设∠BOC=θ,征地面积为f(θ),求f(θ)的表达式,并写出定义域;
(2)当θ满足g(θ)=f(θ)+R2sinθ取得最大值时,开发效果最佳,求出开发效果最佳的角θ的值,并求出g(θ)的最大值.
分析 (1)连结OC,OE,用θ表示出BC,OB,代入梯形面积公式即可得出f(θ);
(2)令sinθ+cosθ=t,使用换元法求出g(θ)的最值及对应的θ.
解答 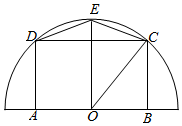 解:(1)连结OE,OC,
解:(1)连结OE,OC,
在Rt△OBC中,BC=Rsinθ,OB=Rcosθ,
∴S梯形OBCE=$\frac{1}{2}$(Rsinθ+R)Rcosθ=$\frac{1}{2}$R2(1+sinθ)cosθ,
∴f(θ)=2S梯形OBCE=R2(1+sinθ)cosθ,θ∈(0,$\frac{π}{2}$).
(2)g(θ)=R2(1+sinθ)cosθ+R2sinθ=R2(sinθ+cosθ+sinθcosθ),
令t=sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),则t∈(1,$\sqrt{2}$],sinθcosθ=$\frac{{t}^{2}-1}{2}$,
∴g(θ)=R2($\frac{{t}^{2}-1}{2}+t$)=$\frac{{R}^{2}}{2}$[(t+1)2-2],
令h(t)=$\frac{{R}^{2}}{2}$[(t+1)2-2],则h(t)在(1,$\sqrt{2}$]上单调递增,
∴当t=$\sqrt{2}$即θ=$\frac{π}{4}$时,h(t)取得最大值($\frac{1}{2}+\sqrt{2}$)R2,
点评 本题考查了函数模型的应用,函数最值的计算,属于中档题.

练习册系列答案
相关题目
18.平面 α∥平面 β,直线 a⊆α,下列四个说法中,正确的个数是
①a与β内的所有直线平行;
②a与β内的无数条直线平行;
③a与β内的任何一条直线都不垂直;
④a与β无公共点.( )
①a与β内的所有直线平行;
②a与β内的无数条直线平行;
③a与β内的任何一条直线都不垂直;
④a与β无公共点.( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.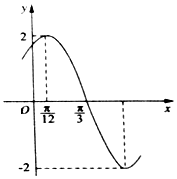 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | 函数f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)的图象关于点(-$\frac{11π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m∈(-2,-$\sqrt{3}$] | |
| D. | 将函数f(x)的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数 |