题目内容
17. 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准0〜3.5,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准0〜3.5,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准0〜3.5,则月均用水量的最低标准定为多少吨,请说明理由;
(3)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).
分析 (1)根据频率和为1计算小组[1.5,2)的频率以及对应小矩形的高;
(2)月均用水量的最低标准应定为2.5吨,此时保证80%的居民每月的用水量不超出标准;
(3)根据频率分布直方图计算这100位居民月均用水量的平均数.
解答 解:(1)根据频率和为1,计算小组[1.5,2)的频率为
1-(0.10+0.20+0.30+0.60+0.30+0.10)×0.5=0.2,
对应小矩形的高为$\frac{0.2}{\frac{1}{2}}$=0.4,把频率分布直方图补充完整如下;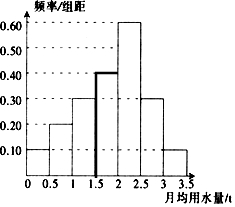
(2)月均用水量的最低标准应定为2.5吨,
样本中月均不低于2.5吨的居民有20位,占样本总体的20%,
由样本估计总体,要保证80%的居民每月的用水量不超出标准,
月均用水量的最低标准应定为2.5吨;
(3)估计频率分布直方图,计算这100位居民月均用水量的平均数为
0.5×($\frac{1}{4}$×0.10+$\frac{3}{4}$×0.20+$\frac{5}{4}$×0.30+$\frac{7}{4}$×0.40+$\frac{9}{4}$×0.60+$\frac{11}{4}$×0.30+$\frac{13}{4}$×0.10)=1.875.
点评 本题考查了频率分布直方图的应用问题,是基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
7.“DD共享单车”是为城市人群提供便捷经济、绿色低碳的环保出行方式,根据日前在三明市的投放量与使用的情况,有人作了抽样调查,抽取年龄在二十至五十岁的不同性别的骑行者,统计数据如下表所示:
(Ⅰ)求统计数据表中a,d的值;
(Ⅱ)假设用抽到的100名20~35岁年龄的骑行者作为样本估计全市的该年龄段男女使用”DD共享单车“情况,现从全市的该年龄段骑行者中随机抽取3人,求恰有一名女性的概率;
(Ⅲ)根据以上列联表,判断使用”DD共享单车“的人群中,能否有95%的把握认为”性别“与”年龄“有关,并说明理由.
参考数表
参考公式K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
| 男性 | 女性 | 合计 | |
| 20~35岁 | a | 40 | 100 |
| 36~50岁 | 40 | d | 90 |
| 合计 | 100 | 90 | 190 |
(Ⅱ)假设用抽到的100名20~35岁年龄的骑行者作为样本估计全市的该年龄段男女使用”DD共享单车“情况,现从全市的该年龄段骑行者中随机抽取3人,求恰有一名女性的概率;
(Ⅲ)根据以上列联表,判断使用”DD共享单车“的人群中,能否有95%的把握认为”性别“与”年龄“有关,并说明理由.
参考数表
| P(K2>k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
12.曲线y=-x3+2x+3在点(1,4)处的切线的斜率为( )
| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
9.圆心在原点,半径为2的圆的渐开线的参数方程是( )
| A. | $\left\{\begin{array}{l}{x=2(cosφ+φsinφ)}\\{y=2(sinφ-φcosφ)}\end{array}\right.$(φ为参数) | |
| B. | $\left\{\begin{array}{l}{x=4(cosθ+θsinθ)}\\{y=4(sinθ-θcosθ)}\end{array}\right.$(θ为参数) | |
| C. | $\left\{\begin{array}{l}{x=2(φ-sinφ)}\\{y=2(1-cosφ)}\end{array}\right.$(φ为参数) | |
| D. | $\left\{\begin{array}{l}{x=4(θ-sinθ)}\\{y=4(1-cosθ)}\end{array}\right.$(θ为参数) |
6.某人将密码“19923”记错密码数字顺序,他可能犯的错误次数最多是(假定错误不重犯)( )
| A. | 120 | B. | 119 | C. | 60 | D. | 59 |
 如图所示,△ABC中,直线PQ与边AB、BC及AC的延长线分别交于点P、M、Q,$\overrightarrow{BM}$=3$\overrightarrow{MC}$,$\overrightarrow{AP}$=$\frac{t}{1-t}$$\overrightarrow{PB}$,$\overrightarrow{AQ}$=s$\overrightarrow{AC}$,则$\frac{1}{t}$+$\frac{3}{s}$=4.
如图所示,△ABC中,直线PQ与边AB、BC及AC的延长线分别交于点P、M、Q,$\overrightarrow{BM}$=3$\overrightarrow{MC}$,$\overrightarrow{AP}$=$\frac{t}{1-t}$$\overrightarrow{PB}$,$\overrightarrow{AQ}$=s$\overrightarrow{AC}$,则$\frac{1}{t}$+$\frac{3}{s}$=4.