题目内容
2.已知f(x)=$\left\{\begin{array}{l}{(3a-1)x+4a,x<1}\\{-{x}^{2}+ax-1,x≥1}\end{array}\right.$是(-∞,+∞)上的减函数,求实数a的取值范围.分析 根据分段函数的单调性建立条件关系进行求解即可.
解答 解:当x<1时,若函数f(x)为减函数,则3a-1<0,即a<$\frac{1}{3}$,①
若当x≥1时,函数f(x)为减函数,则-$\frac{a}{-2}$=$\frac{a}{2}$≤1,即a≤2,②
若f(x)在(-∞,+∞)上为减函数,
则3a-1+4a≥-1+a-1,即a≥-$\frac{1}{6}$,③,
综上-$\frac{1}{6}$≤a<$\frac{1}{3}$.
点评 本题主要考查分段函数单调性的应用,根据分段函数单调性的性质建立不等式关系是解决本题的关键.

练习册系列答案
相关题目
11.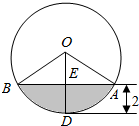 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )| A. | 4-$\frac{3\sqrt{3}}{4π}$ | B. | 2-$\frac{3\sqrt{3}}{16π}$ | C. | 3-$\frac{9\sqrt{3}}{4π}$ | D. | 3-$\frac{9\sqrt{3}}{16π}$ |