题目内容
9.已知cosα是方程3x2-x-2=0的根,且α是第三象限角,则$\frac{sin(-α+\frac{3π}{2})cos(\frac{3π}{2}+α)ta{n}^{2}(π-α)}{cos(\frac{π}{2}+α)sin(\frac{π}{2}-α)}$=( )| A. | $\frac{9}{16}$ | B. | -$\frac{9}{16}$ | C. | -$\frac{5}{4}$ | D. | $\frac{5}{4}$ |
分析 由题意求出cosα的值,进一步求得sinα,得到tanα,然后利用诱导公式化简求得$\frac{sin(-α+\frac{3π}{2})cos(\frac{3π}{2}+α)ta{n}^{2}(π-α)}{cos(\frac{π}{2}+α)sin(\frac{π}{2}-α)}$.
解答 解:由3x2-x-2=0,得x=1或x=$-\frac{2}{3}$,
∵cosα是方程3x2-x-2=0的根,且α是第三象限角,
∴cos$α=-\frac{2}{3}$,sinα=$-\sqrt{1-co{s}^{2}α}=-\sqrt{1-(-\frac{2}{3})^{2}}$=$-\frac{\sqrt{5}}{3}$,tan$α=\frac{\sqrt{5}}{2}$.
则$\frac{sin(-α+\frac{3π}{2})cos(\frac{3π}{2}+α)ta{n}^{2}(π-α)}{cos(\frac{π}{2}+α)sin(\frac{π}{2}-α)}$=$\frac{cosα•sinα•ta{n}^{2}α}{-sinα•cosα}$=-tan2α=$-\frac{5}{4}$.
故选:C.
点评 本题考查三角函数的化简求值,考查同角三角函数的基本关系式及诱导公式的应用,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知f(x)=sinnx,则f′(x)=( )
| A. | nsinn-1x | B. | ncosn-1x | C. | cosnx | D. | nsinn-1x•cosx |
4.某医院准备从6名骨科大夫中选派3名去农村三处医疗所做培训,要求甲、乙两位骨科组长至少有一人参加,那么不同的选派种数为( )
| A. | 96 | B. | 72 | C. | 60 | D. | 30 |
1.在数列{an}中,a1=$\frac{1}{2}$,a2=$\frac{1}{3}$,anan+2=1,则a2016+a2017=( )
| A. | $\frac{5}{6}$ | B. | $\frac{7}{3}$ | C. | $\frac{7}{2}$ | D. | 5 |
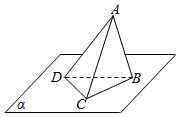 如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.
如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.