题目内容
已知f(a)=
(3a2x2-4ax)dx(a∈R),则f (a)的最小值为 .
| ∫ | 1 0 |
考点:定积分
专题:导数的综合应用
分析:先求出f(a)的表达式,结合二次函数的性质从而求出f(a)的最小值.
解答:
解:∵f(a)=
(3a2x2-4ax)dx
=(a2x3-2ax2)
=a2-2a,
=(a-1)2-1,
≥-1,
故答案为:-1.
| ∫ | 1 0 |
=(a2x3-2ax2)
| | | 1 0 |
=a2-2a,
=(a-1)2-1,
≥-1,
故答案为:-1.
点评:本题考查了定积分的求值问题,考查了二次函数的性质,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
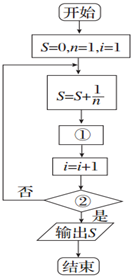 如图给出的是计算1+
如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 9 |
| A、n=n+2,i>5? |
| B、n=n+2,i=5? |
| C、n=n+1,i=5? |
| D、n=n+1,i>5? |
若函数f(x)在R上是单调递减的奇函数,则下列关系式成立的是( )
| A、f(3)<f(4) |
| B、f(3)<-f(-4) |
| C、-f(-3)<f(-4) |
| D、f(-3)>f(-4) |
| ∫ |
-
|
| A、1 | B、0 | C、-1 | D、2 |
函数f(x)=2sin(
-
)+1(x∈R)的最小正周期、最大值依次为( )
| x |
| 2 |
| π |
| 3 |
| A、4π,3 | B、4π,2 |
| C、2π,3 | D、2π,2 |
已知f(x)是偶函数,且在(-∞,0]上是增函数.若f(lnx)<f(1),则x的取值范围是( )
| A、(e,+∞) | ||
B、(
| ||
C、(e,+∞)∪(0,
| ||
D、(
|
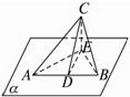 Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.
Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.