题目内容
9.数列{an}的前n项和Sn=2n,数列{bn}满足:b1=-1,bn+1=bn+(2n-1).(n∈N*)(1)求数列{an}的通项an;
(2)求数列{bn}的通项bn.
分析 (1)由an=Sn-Sn-1求出n≥2时的通项公式,已知首项后得答案;
(2)直接利用累加法求数列{bn}的通项bn.
解答 解:(1)∵Sn=2n,
∴Sn-1=2n-1,(n≥2),
∴${a}_{n}={S}_{n}-{S}_{n-1}={2}^{n}-{2}^{n-1}={2}^{n-1}(n≥2)$,
当n=1时,a1=S1=2不适合上式,
∴${a}_{n}=\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$;
(2)由bn+1=bn+(2n-1),
得b2=b1+1,b3=b2+3,…,bn=bn-1+2n-3(n≥2),
累加得:bn=b1+[1+3+…+(2n-3)]=$-1+\frac{(1+2n-3)(n-1)}{2}={n}^{2}-2n$(n≥2).
b1=-1适合上式,
∴${b}_{n}={n}^{2}-2n$.
点评 本题考查数列递推式,训练了累加法求数列的通项公式,是中档题.

练习册系列答案
相关题目
17.曲线y=tanx在点($\frac{π}{4}$,1)处的切线的斜率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
4.已知关于x的方程x2+(a2-1)x+a-2=0的一个根比1大,另一个根比1小,则实数a的取值范围是( )
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-2,1) | D. | (-∞,-2)∪(1,+∞) |
18.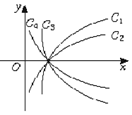 图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
 图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )| A. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | B. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{1}{10}$,$\frac{3}{5}$ | C. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | D. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{1}{10}$,$\frac{3}{5}$ |