题目内容
点P在曲线y=lnx+2上运动，点Q在直线x-y+4=0上运动，则P，Q两点的最短距离是 ．
考点：利用导数研究曲线上某点切线方程,两条平行直线间的距离
专题：导数的综合应用
分析：利用平移切线法求出切点坐标，利用点到直线的距离公式即可得到结论．
解答：
解：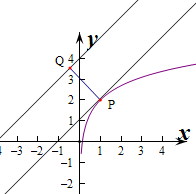
设和x-y+4=0平行且和曲线y=lnx+2相切的直线为l：则l的斜率k=1，
∵y=lnx+2，
∴y′=f′（x）=
，
由y′=f′（x）=
=1，x=1，
此时y=2+ln1=2，即切点P的坐标为（1，2），
则P到直线x-y+4=0的距离d=
=
=
，
∴P，Q两点的最短距离|PQ|=
，
故答案为：
．
设和x-y+4=0平行且和曲线y=lnx+2相切的直线为l：则l的斜率k=1，∵y=lnx+2，
∴y′=f′（x）=
| 1 |
| x |
由y′=f′（x）=
| 1 |
| x |
此时y=2+ln1=2，即切点P的坐标为（1，2），
则P到直线x-y+4=0的距离d=
| |1-2+4| | ||
|
| 3 | ||
|
3
| ||
| 2 |
∴P，Q两点的最短距离|PQ|=
3
| ||
| 2 |
故答案为：
3
| ||
| 2 |
点评：本题主要考查两点间距离的求法，利用平移切线法是解决本题的关键，综合考查了导数在求最值中的利用，综合性较强．
练习册系列答案
相关题目
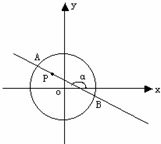圆x2+y2=8内有一点P（-1，2），AB为过点P且倾斜角为α的弦，点A（2，5）到直线l：x-2y+3=0的距离为（ ）
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|