题目内容
15.函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是[1,3].分析 根据题意,由函数奇偶性的性质可得f(-1)=1,利用函数的单调性可得-1≤x-2≤1,解可得x的取值范围,即可得答案.
解答 解:根据题意,f(x)为奇函数,若f(1)=-1,则f(-1)=1,
f(x)在(-∞,+∞)单调递减,且-1≤f(x-2)≤1,即f(1)≤f(x-2)≤f(-1),
则有-1≤x-2≤1,
解可得1≤x≤3,
即x的取值范围是[1,3];
故答案为:[1,3].
点评 本题考查函数奇偶性与单调性的综合应用,关键是将-1≤f(x-2)≤1转化为关于x的不等式.

练习册系列答案
相关题目
10.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
| A. | 0.312 | B. | 0.36 | C. | 0.432 | D. | 0.648 |
12.若函数$f(x)=4sinωx•{sin^2}({\frac{ωx}{2}+\frac{π}{4}})-2{sin^2}ωx(ω>0)$在$[{-\frac{π}{2},\frac{2π}{3}}]$上是增函数,则ω的取值范围是( )
| A. | (0,1] | B. | $({0,}\right.\left.{\frac{3}{4}}]$ | C. | [1,+∞) | D. | $[{\frac{3}{4}}\right.,+∞)$ |
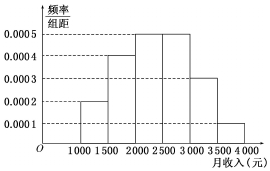 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)). 如图,在三棱柱ABC-A1B1C1中,AB⊥BC,顶点A1在底面ABC内的射影恰好是AB的中点O,且AB=BC=2.OA1=2,
如图,在三棱柱ABC-A1B1C1中,AB⊥BC,顶点A1在底面ABC内的射影恰好是AB的中点O,且AB=BC=2.OA1=2,