题目内容
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若过F且倾斜角为60°的直线分别与双曲线的左右两支相交,则此双曲线离心率的取值范围是(2,+∞).分析 根据已知直线的斜率,求出渐近线的斜率范围,推出a,b的关系,然后求出离心率的范围.
解答 解:依题意,斜率为$\sqrt{3}$的直线l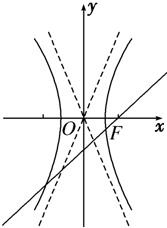 过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)
过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)
的右焦点为F且与双曲线的左右两支分别相交,
结合图形分析可知,
双曲线的一条渐近线的斜率$\frac{b}{a}$必大于$\sqrt{3}$,
即$\frac{b}{a}$>$\sqrt{3}$,
因此该双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$>$\sqrt{1+3}$=2.
故答案为:(2,+∞).
点评 本题考查直线的斜率,双曲线的应用,考查转化思想,是基础题.

练习册系列答案
相关题目
7.如图是一个算法的流程图,则输出的a值为( )


| A. | 511 | B. | 1023 | C. | 2047 | D. | 4095 |
8.已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)在区间$[{\frac{π}{6},\frac{π}{2}}]$上单调递增,且函数值从-2增大到0.若${x_1}_{\;}、{x_2}∈[{-\frac{π}{6},\frac{π}{2}}]$,且f(x1)=f(x2),则f(x1+x2)=( )
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
12.已知命题p:?x∈R,x2-x+1<0,则¬p是( )
| A. | ?x∈R,x2-x+1<0 | B. | ?x∈R,x2-x+1≥0 | C. | ?x∈R,x2-x+1<0 | D. | ?x∈R,x2-x+1≥0 |
2.若直线l与直线3x+y+8=0垂直,则直线l的斜率为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
7.下列函数中,最小正周期为π且为奇函数的是( )
| A. | y=sin$\frac{x}{2}$ | B. | y=cos$\frac{x}{2}$ | C. | y=cos2x | D. | y=sin2x |
 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000m,速度为1000km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为6340m.(取$\sqrt{3}$=1.732)
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000m,速度为1000km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为6340m.(取$\sqrt{3}$=1.732)