题目内容
椭圆
+
=1（a＞b＞0）的两焦点为F1（0，-c），F2（0，c）（c＞0），离心率e=
，焦点到椭圆上点的最短距离为2-
，求椭圆的方程．
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| 3 |
考点：椭圆的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据题意建立关于a、c的方程组，解出a=2且c=
，从而得到b2=a2-c2=1，可得椭圆的方程
| 3 |
解答：
解：∵e=
，焦点到椭圆上点的最短距离为2-
，
∴
=
，a-c=2-
，
解得a=2，c=
，
∴b2=a2-c2=1，
由此可得椭圆的方程为
+x2=1．
| ||
| 2 |
| 3 |
∴
| c |
| a |
| ||
| 2 |
| 3 |
解得a=2，c=
| 3 |
∴b2=a2-c2=1，
由此可得椭圆的方程为
| y2 |
| 4 |
点评：本题已知椭圆满足的条件，求椭圆的方程，着重考查了椭圆的定义与标准方程等知识，属于基础题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知F1（-3，0），F2（3，0），是椭圆
+
=1（a＞b＞0）两个焦点，P在椭圆上，∠F1PF2=α，且当α=
时，△F1PF2的面积最大，则椭圆的标准方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
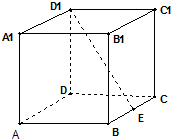如图在棱长为2的正方体ABCD-A1B1C1D1中E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从0，1，2，3中选取三个不同的数字组成一个三位数，则不同的三位数有（ ）
| A、24个 | B、20个 |
| C、18个 | D、15个 |
