题目内容
16.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为抛物线C2:y2=2px的焦点F,且点F到双曲线的一条渐近线的距离为$\sqrt{3}$,若双曲线C1与抛物线C2在第一象限内的交点为P(x0,2$\sqrt{6}$),则该双曲线的离心率e为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
分析 利用已知条件求出b,通过交点坐标,代入抛物线以及双曲线方程,转化求解双曲线的离心率即可.
解答 解:双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为抛物线C2:y2=2px的焦点F,可得$\frac{p}{2}$=c,
点F到双曲线的一条渐近线bx+ay=0的距离为$\sqrt{3}$,可得$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}=\sqrt{3}$,b=$\sqrt{3}$,
双曲线C1与抛物线C2在第一象限内的交点为P(x0,2$\sqrt{6}$),
可得:24=2px0,$\frac{{{x}_{0}}^{2}}{{a}^{2}}-\frac{24}{3}=1$,
可得:a2c2=4,b2=3,
可得a=1,c=2.
双曲线的离心率为:2.
故选:B.
点评 本题考查双曲线的简单性质的应用,抛物线的简单性质的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若sinαsinβ=1,则cos(α+β)=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 0或-1 |
11.已知集合A={x|y=log2x,y∈Z},B={1,2,3,4,5,6,7,8,9},则A∩B=( )
| A. | {1,2,3,4} | B. | {2,4,6,8} | C. | {1,2,4,8} | D. | {2,4,8} |
1.101(9)化为十进制数为( )
| A. | 9 | B. | 11 | C. | 82 | D. | 101 |
8.在△ABC中,角A、B、C的对边分别为a,b,c,且b(2sinB+sinA)+(2a+b)sinA=2csinC,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
6. 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )| A. | 65 | B. | 64 | C. | 63 | D. | 62 |
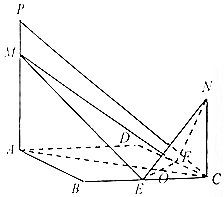 如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.
如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.