题目内容
已知数列{an}满足a1=1,n(an+1-an)=an+n2+n,n∈N*.
(1)证明:数列{
}是等差数列;
(2)设an=(
)2,求正项数列{bn}的前n项和Sn.
(1)证明:数列{
| an |
| n |
(2)设an=(
| 2nbn |
| 32n+1 |
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)由已知得nan+1=(n+1)an+n2+n,n∈N*,从而
-
=1,
=1,由此能证明数列{
}是以1为首项,以1为公差的等差数列.
(2)由an=n2,得an=(
)2=n2,正项数列{bn},从而bn=
×32n+1,由此能求出正项数列{bn}的前n项和Sn.
| an+1 |
| n+1 |
| an |
| n |
| a1 |
| 1 |
| an |
| n |
(2)由an=n2,得an=(
| 2nbn |
| 32n+1 |
| 1 |
| 2 |
解答:
(1)证明:∵数列{an}满足a1=1,n(an+1-an)=an+n2+n,n∈N*,
∴nan+1=(n+1)an+n2+n,n∈N*,
∴
-
=1,
=1,
∴数列{
}是以1为首项,以1为公差的等差数列.
(2)解:∵数列{
}是以1为首项,以1为公差的等差数列,
∴
=n,∴an=n2,
∴an=(
)2=n2,正项数列{bn},
∴bn=
×32n+1,
∴Sn=
(33+35+…+32n+1)
=
×
=-
(1-9n).
∴nan+1=(n+1)an+n2+n,n∈N*,
∴
| an+1 |
| n+1 |
| an |
| n |
| a1 |
| 1 |
∴数列{
| an |
| n |
(2)解:∵数列{
| an |
| n |
∴
| an |
| n |
∴an=(
| 2nbn |
| 32n+1 |
∴bn=
| 1 |
| 2 |
∴Sn=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 27(1-9n) |
| 1-9 |
=-
| 27 |
| 16 |
点评:本题考查等差数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意构造法和等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本的平均重量为( )

| A、13 | B、12 | C、11 | D、10 |
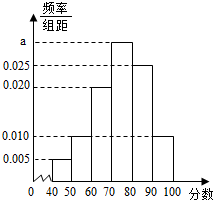 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.