[题目]已知椭圆的一个顶点为A(2.0).离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M.N.(1)求椭圆C的方程.(2)当△AMN的面积为时.求k的值. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆的一个顶点为A(2，0)，离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M、N.
（1）求椭圆C的方程.
（2）当△AMN的面积为时，求k的值.

【答案】
（1）解：由题意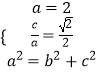得，解得，所以椭圆C的方程为
（2）解：由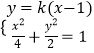，得，
设点M、N的坐标分别为，则，，，所以

又因为点到直线的距离，所以的面积为，
由得，
【解析】（1）运用离心率公式和a，b，c的关系，解得b，进而得到椭圆方程；
（2）联立直线方程和椭圆方程，消去y，运用韦达定理和配方，化简整理，解方程即可得到k．本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、三角形面积计算公式、点到直线的距离公式，考查了推理能力与计算能力，属于中档题．
【考点精析】根据题目的已知条件，利用椭圆的标准方程的相关知识可以得到问题的答案，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：．

练习册系列答案

相关题目

【题目】70年代中期，美国各所名牌大学校园内，人们都像发疯一般，夜以继日，废寝忘食地玩一个数学游戏．这个游戏十分简单：任意写出一个自然数N，并且按照以下的规律进行变换：如果是个奇数，则下一步变成3N+1；如果是个偶数，则下一步变成．不单单是学生，甚至连教师、研究员、教授与学究都纷纷加入．为什么这个游戏的魅力经久不衰？因为人们发现，无论N是怎样一个数字，最终都无法逃脱回到谷底1．准确地说，是无法逃出落入底部的4﹣2﹣1循环，永远也逃不出这样的宿命．这就是著名的“冰雹猜想”．按照这种运算，自然数27经过十步运算得到的数为（）
A.142
B.71
C.214
D.107

【题目】已知圆过圆与直线的交点，且圆上任意一点关于直线的对称点仍在圆上．

（1）求圆的标准方程；

（2）若圆与轴正半轴的交点为，直线与圆交于两点(异于点)，且点满足,,求直线的方程．

【题目】已知抛物线的焦点为，是抛物线上横坐标为4，且位于轴上方的点，到抛物线准线的距离等于5，过作垂直于轴，垂足为，的中点为．
（1）求抛物线的方程；
（2）若过作，垂足为，求点的坐标．

【题目】已知函数f（x）=lnx﹣a（x﹣1），g（x）=ex ．
（1）求函数f（x）的单调区间；
（2）当a≠0时，过原点分别作曲线y=f（x）与y=g（x）的切线l1 ， l2 ，已知两切线的斜率互为倒数，证明：＜a＜；
（3）设h（x）=f（x+1）+g（x），当x≥0，h（x）≥1时，求实数a的取值范围．