题目内容
11.如图,在三棱锥P-ABC中,三组对棱相等,且PA=13,PB=14,PC=15,求三棱锥的体积.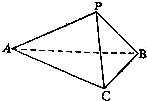
分析 由三棱锥的各面全等可知三棱锥可看做长方体切去四个小棱锥得到的,长方体的面对角线为13,14,15,求出长方体的棱长,使用作差法求出体积.
解答 解:由题意可知三棱锥的四个面全等.
故三棱锥可看做是对角线为13,14,15的长方体的面对角线组成的棱锥.
设长方体的棱长分别为a,b,c,则$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=169}\\{{a}^{2}+{c}^{2}=196}\\{{b}^{2}+{c}^{2}=225}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=70}\\{{b}^{2}=99}\\{{c}^{2}=126}\end{array}\right.$.
∴长方体的体积V长方体=abc=$\sqrt{{a}^{2}{b}^{2}{c}^{2}}$=126$\sqrt{55}$.
∴三棱锥的体积为V=V长方体-4×$\frac{1}{3}×\frac{1}{2}abc$=$\frac{1}{3}{V}_{长方体}$=42$\sqrt{55}$.
点评 本题考查了棱锥的体积计算,发现棱锥的特点是解题关键,属于中档题.

练习册系列答案
相关题目

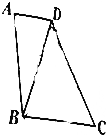 在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.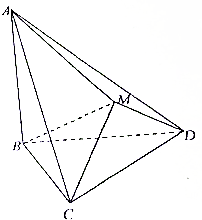 如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.
如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.