题目内容
15.给出四个命题:①若x2-3x+2=0,则x=1或x=2;
②若x=y=0,则x2+y2=0;
③已知x,y∈N,若x+y是奇数,则x,y中一个是奇数,一个偶数;
④若x1,x2是方程x2-2$\sqrt{3}$x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率.
那么( )
| A. | ①的逆命题为真 | B. | ②的否命题为假 | C. | ③的逆命题为假 | D. | ④的逆否命题为假 |
分析 写出命题①的逆命题并判断真假判断A;写出命题②的否命题并判断真假判断B;写出命题③的逆命题并判断真假判断C;真假判断④的真假判断D.
解答 解:对于①,若x2-3x+2=0,则x=1或x=2,其逆命题为:若x=1或x=2,则x2-3x+2=0,是真命题,原因是x=1,x=2是方程的两根;
对于②,若x=y=0,则x2+y2=0的逆命题为:若x2+y2=0,则x=y=0,是真命题,
∵一个命题的逆命题与否命题互为逆否命题,共真假,∴若x=y=0,则x2+y2=0的否命题也是真命题;
对于③,已知x,y∈N,若x+y是奇数,则x,y中一个是奇数,一个偶数的逆命题为:已知x,y∈N,若x,y中一个是奇数,一个偶数,则x+y是奇数,为真命题;
对于④,方程x2-2$\sqrt{3}$x+2=0的两根$x=\frac{2\sqrt{3}±2}{2}=\sqrt{3}±1$,则x1,x2可以是一椭圆与一双曲线的离心率,
∴命题若x1,x2是方程x2-2$\sqrt{3}$x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率为真命题,则其逆否命题也为真命题.
综上可知,①的逆命题为真.
故选:A.
点评 本题考查命题的真假判断与应用,考查了原命题、逆命题、否命题、逆否命题的写法与真假判断,是中档题.

练习册系列答案
相关题目
7.已知{an}为等比数列,若a1+a4=8,a3+a6=2,则公比q的值为( )
| A. | ±2 | B. | $±\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
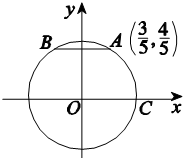 如图所示,A,B是单位圆O上的点,且B在第二象限,C是圆与x轴正半轴的交点,A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),且A与B关于y轴对称.
如图所示,A,B是单位圆O上的点,且B在第二象限,C是圆与x轴正半轴的交点,A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),且A与B关于y轴对称.