题目内容
12.已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),右顶点为D(2,0),设点A(1,0.5).(1)求该椭圆的标准方程;
(2)若P是椭圆上的动点,求线段PA中点M的轨迹方程.
分析 (1)由题意可知:椭圆的焦点在x轴上,设$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),由a=2,c=$\sqrt{3}$,b2=a2-c2=1,即可求得该椭圆的标准方程;
(2)设线段PA的中点为M(x,y),点P的坐标是(x0,y0),由中点坐标公式可知:$\left\{\begin{array}{l}{x=\frac{{x}_{0}+1}{2}}\\{y=\frac{{y}_{0}+\frac{1}{2}}{2}}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{{x}_{0}=2x-1}\\{{y}_{0}=2y-\frac{1}{2}}\end{array}\right.$,将P代入椭圆方程,即可求得线段PA中点M的轨迹方程.
解答 解:(1)由题意可知:椭圆的焦点在x轴上,设$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由椭圆的左焦点为F(-$\sqrt{3}$,0),右顶点为D(2,0),即a=2,c=$\sqrt{3}$,
则b2=a2-c2=1,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;------------------(5分)
(2)设线段PA的中点为M(x,y),点P的坐标是(x0,y0),------------------------(6分)
由中点坐标公式可知:$\left\{\begin{array}{l}{x=\frac{{x}_{0}+1}{2}}\\{y=\frac{{y}_{0}+\frac{1}{2}}{2}}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{{x}_{0}=2x-1}\\{{y}_{0}=2y-\frac{1}{2}}\end{array}\right.$,------------(8分)
由点P在椭圆上,
∴$\frac{(2x-1)^{2}}{4}+(2y-\frac{1}{2})^{2}=1$,---------(10分)
∴线段PA中点M的轨迹方程是:(x-$\frac{1}{2}$)2+4(y-$\frac{1}{4}$)2=1.------(12分)
点评 本题考查椭圆的标准方程与性质,考查轨迹方程的求法,中点坐标公式的应用,考查计算能力,属于中档题.

 在几何体EFABCD中,矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,且AB∥EF,AB=2EF,设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值为( )
在几何体EFABCD中,矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,且AB∥EF,AB=2EF,设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值为( )| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 5:1 |
| A. | 24 | B. | 32 | C. | 36 | D. | 40 |
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{3}$ |
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
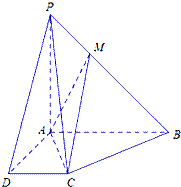 如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.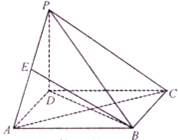 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,