题目内容
3.集合M={x|x2-2x≥3},集合N={x|x2-6x+8<0},则M∩N=( )| A. | [3,4) | B. | (2,3] | C. | (-1,2) | D. | (-1,3] |
分析 求出M与N中不等式的解集分别确定出M与N,求出两集合的交集即可.
解答 解:由M中不等式变形得:(x-3)(x+1)≥0,
解得:x≤-1或x≥3,即M=(-∞,-1]∪[3,+∞),
由N中不等式变形得:(x-2)(x-4)<0,
解得:2<x<4,即N=(2,4),
则M∩N=[3,4),
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
14.下列命题中错误的是( )
| A. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| B. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| C. | 如果直线a∥平面α,那么a平行于平面α内的无数条直线 | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
15.若$\frac{cos2α}{sin(α-\frac{π}{4})}$=-$\frac{\sqrt{2}}{2}$,则sin(α+$\frac{π}{4}$)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{2}}{4}$ |
13.在面积为1的等边三角形ABC内任取一点,使三角形△ABP,△ACP,△BCP的面积都小于$\frac{1}{2}$的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
 如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC,点E,F分别是BC,A1C的中点.
如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC,点E,F分别是BC,A1C的中点.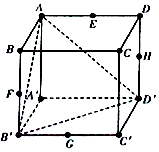 已知立方体ABCD-A'B'C'D',E,F,G,H分别是棱AD,BB',B'C',DD'中点,从中任取两点确定的直线中,与平面AB'D'平行的有( )条.
已知立方体ABCD-A'B'C'D',E,F,G,H分别是棱AD,BB',B'C',DD'中点,从中任取两点确定的直线中,与平面AB'D'平行的有( )条.