题目内容
在数列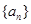 中,
中,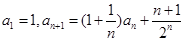 ,
,
(I)求数列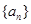 的通项公式;
的通项公式;
(II)求数列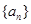 的前
的前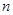 项和
项和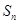
(1)  (2)
(2)  =
=

解析试题分析:解:(I)由已知有
 利用累差迭加即可求出数列
利用累差迭加即可求出数列 的通项公式:
的通项公式:  (
( )
)
(II)由(I)知 ,
,
 =
=

而 ,又
,又 是一个典型的错位相减法模型,
是一个典型的错位相减法模型,
易得

 =
=

考点:数列的通项公式和求和的运用
点评:解决的关键是对于数列的递推关系式的运用,根据迭代法得到通项公式,并结合错位相减法求和。

练习册系列答案
相关题目
[2014·北京模拟]数列{xn}中,若x1=1,xn+1= -1,则x2014=( )
-1,则x2014=( )
| A.-1 | B.- | C. | D.1 |
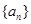 的前n项和为
的前n项和为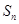 ,已知
,已知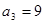 ,
, 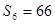 .
.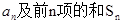 ;
;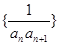 的前n项和为
的前n项和为 ,证明:
,证明: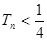 ;
;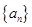 的前n项和记为
的前n项和记为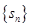 ,已知
,已知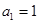 ,
,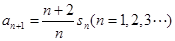 .
.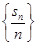 是等比数列;
是等比数列;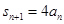 .
. 满足:
满足: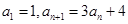 ;
;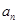 ;
;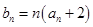 ,求数列
,求数列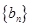 的前
的前 项和为
项和为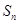 。
。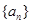 是等差数列,
是等差数列,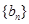 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且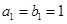 ,
,  ,
,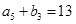
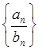 的前n项和
的前n项和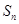 .
.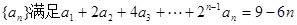 .
.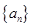 的通项公式;
的通项公式;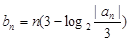 ,探求使
,探求使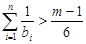 恒成立的
恒成立的 的最大整数值.
的最大整数值.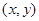 是区域
是区域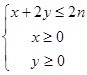 ,(
,(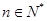 )内的点,目标函数
)内的点,目标函数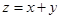 ,
, 的最大值记作
的最大值记作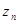 .若数列
.若数列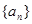 的前
的前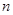 项和为
项和为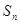 ,
,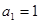 ,且点(
,且点(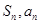 )在直线
)在直线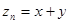 上.
上. 为等比数列;
为等比数列;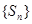 的前
的前 .
.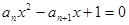 ,
,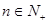 有两根
有两根 和
和 ,且满足
,且满足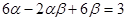 ,
, 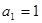
 表示
表示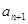 ; (2)证明
; (2)证明 是等比数列;
是等比数列; ,
,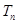 为
为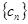 的前n项和,证明
的前n项和,证明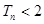 ,(
,(