题目内容
9．已知正方体的外接球的半径为3，则该正方体的棱长为2$\sqrt{3}$．分析 球的直径就是正方体的对角线的长度，然后求出正方体的棱长．
解答 解：正方体外接球的半径R=3，正方体的对角线的长为6，棱长为a，则
$\sqrt{3}$a=6，∴a=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．
点评 本题考查球的内接正方体问题，解答的关键是利用球的直径就是正方体的对角线．是基础题．
练习册系列答案
相关题目
20．
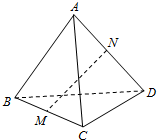如图，在四面体ABCD，AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°，则MN和CD所成的角的大小为（ ）
如图，在四面体ABCD，AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°，则MN和CD所成的角的大小为（ ）| A． | 30° | B． | 60° | C． | 30°或60° | D． | 15°或60° |
如图，已知线段AB在平面α内，线段AC⊥α，线段BD⊥AB，且AB=7，AC=BD=24，CD=25，求线段BD与平面α所成的角30°．
4．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{4}x，x＞0}\\{{2}^{-x}，x≤0}\end{array}\right.$，则f（f（-4））+f（log2$\frac{1}{6}$）=（ ）
| A． | $\frac{1}{2}$ | B． | 3 | C． | 8 | D． | 9 |
14．若p：a＜1，q：关于x的二次方程x2+（a+1）x+a-2=0的一个根大于零，另一根小于零，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
1．
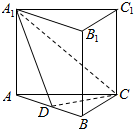如图，三棱柱ABC-A1B1C1的棱长都相等，侧棱垂直于底面，点D是棱AB的中点，则直线AC与平面A1DC所成角的正弦值为（ ）
如图，三棱柱ABC-A1B1C1的棱长都相等，侧棱垂直于底面，点D是棱AB的中点，则直线AC与平面A1DC所成角的正弦值为（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{6}}{4}$ |