题目内容
已知抛物线C的方程为y2=4x.
(Ⅰ)写出焦点F的坐标和准线l的方程;
(Ⅱ)设过点F的直线l与抛物线C相交于A,B两点.问是否存在直线l,使得弦AB的中点为(1,1),若存在,求出直线l的方程;若不存在,请说明理由.
(Ⅰ)写出焦点F的坐标和准线l的方程;
(Ⅱ)设过点F的直线l与抛物线C相交于A,B两点.问是否存在直线l,使得弦AB的中点为(1,1),若存在,求出直线l的方程;若不存在,请说明理由.
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据抛物线方程求得p,则根据抛物线性质可求得抛物线的焦点F的坐标和准线l的方程;
(Ⅱ)利用点差法,结合弦中点的坐标求出斜率,利用点斜式,可得直线l的方程.
(Ⅱ)利用点差法,结合弦中点的坐标求出斜率,利用点斜式,可得直线l的方程.
解答:
解:(Ⅰ)抛物线y2=4x的焦点在x轴上,且p=2
∴抛物线焦点坐标为(1,0),抛物线的准线方程是x=-1.
(Ⅱ)设A(x1,y1),B(x2,y2),则y12=4x1,y22=4x2,
两式相减可得y12-y22=4x1-4x2,
∴(y1+y2)(y1-y2)=4(x1-x2)
∵弦AB的中点为(1,1),
∴y1+y2=2,
∴直线l的斜率为
=2,
∴直线l的方程为y-1=2(x-1),即2x-y-1=0.
∴抛物线焦点坐标为(1,0),抛物线的准线方程是x=-1.
(Ⅱ)设A(x1,y1),B(x2,y2),则y12=4x1,y22=4x2,
两式相减可得y12-y22=4x1-4x2,
∴(y1+y2)(y1-y2)=4(x1-x2)
∵弦AB的中点为(1,1),
∴y1+y2=2,
∴直线l的斜率为
| y1-y2 |
| x1-x2 |
∴直线l的方程为y-1=2(x-1),即2x-y-1=0.
点评:本小题主要考查抛物线的标准方程、抛物线的简单性质等基础知识,考查运算求解能力,考查数形结合思想.属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
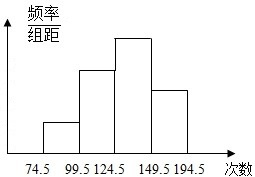 为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题:
为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题: 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0). 某校高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),现用分层抽样的方法选取x名学生参加某项课外活动,已知从身高在[160,170)的学生中选取9人,则x=
某校高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),现用分层抽样的方法选取x名学生参加某项课外活动,已知从身高在[160,170)的学生中选取9人,则x=