题目内容
(本小题满分10分)
已知
 且
且
(1) 求 的定义域;
的定义域;
(2) 判断 的奇偶性;
的奇偶性;
(3)求使得 的
的 的取值范围.
的取值范围.
已知

 且
且
(1) 求
 的定义域;
的定义域;(2) 判断
 的奇偶性;
的奇偶性;(3)求使得
 的
的 的取值范围.
的取值范围.解:(1) 的定义域为
的定义域为 ;(2)
;(2)  为奇函数;
为奇函数;
(3)当 时,
时, ;当
;当 时,
时, 。
。
 的定义域为
的定义域为 ;(2)
;(2)  为奇函数;
为奇函数; (3)当
 时,
时, ;当
;当 时,
时, 。
。本试题主要是考查了函数定义域和函数的奇偶性的运用,以及函数与不等式的求解的综合运用。
(1)因为函数的定义域就是使得原式有意义的自变量的取值范围。
(2)而函数的奇偶性的判定先看定义域是否关于原点对称,然后判定f(x)与f(-x的关系得到结论。
(3)由于底数不定需要对a分情况讨论,得到不等式的解集。
解:(1)要使函数有意义,则 ,即
,即 ,得
,得
所以 的定义域为
的定义域为 ………3分
………3分
(2) 函数的定义域关于原点对称, 又 ,
,
所以 , 所以
, 所以 为奇函数. ………6分
为奇函数. ………6分
(3)当 时,
时, 则
则 ; ………8分
; ………8分
当 时,
时, 则
则 ………10分
………10分
(1)因为函数的定义域就是使得原式有意义的自变量的取值范围。
(2)而函数的奇偶性的判定先看定义域是否关于原点对称,然后判定f(x)与f(-x的关系得到结论。
(3)由于底数不定需要对a分情况讨论,得到不等式的解集。
解:(1)要使函数有意义,则
 ,即
,即 ,得
,得
所以
 的定义域为
的定义域为 ………3分
………3分(2) 函数的定义域关于原点对称, 又
 ,
,所以
 , 所以
, 所以 为奇函数. ………6分
为奇函数. ………6分(3)当
 时,
时, 则
则 ; ………8分
; ………8分当
 时,
时, 则
则 ………10分
………10分
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
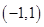 上的函数
上的函数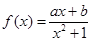 为奇函数,且
为奇函数,且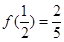
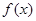 的解析式;
的解析式;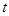 的不等式
的不等式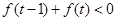 .
.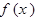 为奇函数。且满足
为奇函数。且满足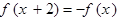 ,当
,当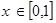 时,
时,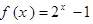 ,则
,则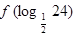 =
= 

 时,求f(x)的单调区间;
时,求f(x)的单调区间; ,若
,若 分别为
分别为 的极大值和极小值,若
的极大值和极小值,若 ,求
,求 取值范围。
取值范围。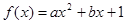 ,
,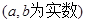 ,
,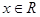 .
.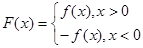
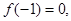 且函数
且函数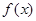 的值域为
的值域为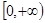 ,求
,求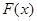 的表达式;
的表达式;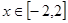 时,
时,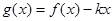 是单调函数,求实数
是单调函数,求实数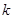 的取值范围;
的取值范围;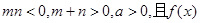 为偶函数,判断
为偶函数,判断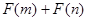 能否大于零?
能否大于零?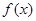 的定义域为
的定义域为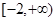 ,部分对应值如下表.
,部分对应值如下表.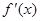 为
为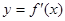 的图像如图
的图像如图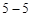 所示:若两正数
所示:若两正数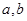 满足
满足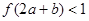 ,则
,则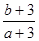 的取值范围是( )
的取值范围是( )





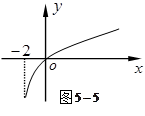
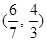 B.
B.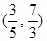 C.
C.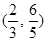 D.
D.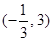
 ”:当a≥b时,a
”:当a≥b时,a 满足
满足 ,当x∈(0,1]时,
,当x∈(0,1]时, ,设
,设

 ,则a,b,c大小关系是( )
,则a,b,c大小关系是( ) , 则
, 则 ( )
( )