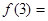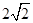题目内容
已知函数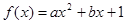 ,
,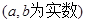 ,
,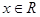 .
.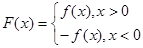
(1)若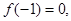 且函数
且函数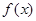 的值域为
的值域为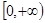 ,求
,求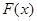 的表达式;
的表达式;
(2)在(1)的条件下,当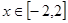 时,
时,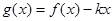 是单调函数,求实数
是单调函数,求实数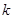 的取值范围;
的取值范围;
(3)设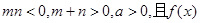 为偶函数,判断
为偶函数,判断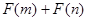 能否大于零?
能否大于零?
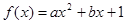 ,
,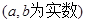 ,
,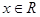 .
.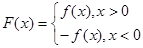
(1)若
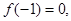 且函数
且函数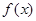 的值域为
的值域为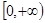 ,求
,求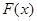 的表达式;
的表达式;(2)在(1)的条件下,当
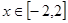 时,
时,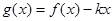 是单调函数,求实数
是单调函数,求实数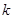 的取值范围;
的取值范围;(3)设
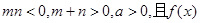 为偶函数,判断
为偶函数,判断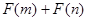 能否大于零?
能否大于零?(1) 
 . (2)
. (2)  是单调函 (3)
是单调函 (3)  能大于零.
能大于零.

 . (2)
. (2)  是单调函 (3)
是单调函 (3)  能大于零.
能大于零.本试题主要是考查了二次函数与分段函数的单调性和不等式的求解的综合运用。
(1)根据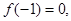 且函数
且函数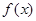 的值域为
的值域为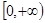 ,得到结论。
,得到结论。
(2)因为 是二次函数,利用对称轴和定义域得到结论。
是二次函数,利用对称轴和定义域得到结论。
(3) 是偶函数,
是偶函数,



 分析证明之。
分析证明之。
(1) 恒成立, ……………1分
恒成立, ……………1分
 ,解得
,解得

 . …………4分
. …………4分
(2)
当 ,即
,即 是单调函 ………8分
是单调函 ………8分
(3) 是偶函数,
是偶函数, …………9分
…………9分




于是有
 能大于零.
能大于零.
(1)根据
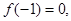 且函数
且函数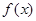 的值域为
的值域为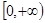 ,得到结论。
,得到结论。(2)因为
 是二次函数,利用对称轴和定义域得到结论。
是二次函数,利用对称轴和定义域得到结论。(3)
 是偶函数,
是偶函数,



 分析证明之。
分析证明之。(1)
 恒成立, ……………1分
恒成立, ……………1分 ,解得
,解得

 . …………4分
. …………4分 (2)

当
 ,即
,即 是单调函 ………8分
是单调函 ………8分(3)
 是偶函数,
是偶函数, …………9分
…………9分



于是有

 能大于零.
能大于零.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
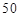 至
至 人之间,游客人数
人之间,游客人数 (人)与游客的消费总额
(人)与游客的消费总额 (元)之间近似地满足关系:
(元)之间近似地满足关系: .那么游客的人均消费额最高为_________元
.那么游客的人均消费额最高为_________元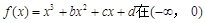 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程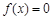 有三个根,它们分别为
有三个根,它们分别为 .
. ;
; 的取值范围.
的取值范围.
 且
且
 的定义域;
的定义域; 的
的 的取值范围.
的取值范围. 是偶函数,则函数图像与
是偶函数,则函数图像与 轴交点的纵坐标的最大值是______.
轴交点的纵坐标的最大值是______. 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元; 元的超额费;
元的超额费; (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式; 的值。
的值。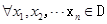 ,都有
,都有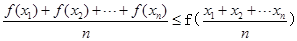 ,若
,若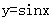 在区间
在区间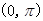 上是凸函数,那么在
上是凸函数,那么在 中,
中,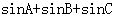 的最大值为( )
的最大值为( )



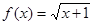 则
则