题目内容
14.$\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{DB}$=( )| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{BD}$ |
分析 根据平面向量减法的三角形法则计算.
解答 解:$\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{DB}$=$\overrightarrow{CB}-\overrightarrow{DB}$=$\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{CD}$.
故选C.
点评 本题考查了平面向量线性运算的几何意义,属于基础题.

练习册系列答案
相关题目
4.已知M(x0,y0)是双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1上的一点,F1,F2是双曲线C的两个焦点,若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$≤0,则M到坐标原点的距离|MO|的最大值为( )
| A. | 4 | B. | 5 | C. | 3 | D. | 2$\sqrt{5}$ |
9.如图所示的是函数y=2sin(ωx+φ)(|φ|<$\frac{π}{2}$)的部分图象,那么( )
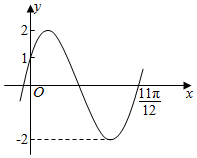

| A. | ω=$\frac{10}{11}$,φ=$\frac{π}{6}$ | B. | ω=$\frac{10}{11}$,φ=-$\frac{π}{6}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=2,φ=-$\frac{π}{6}$ |
4.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,若抛物线C2:y2=2px(p>0)的焦点到双曲线C1的渐近线的距离为$\sqrt{2}$,则抛物线C2的方程为( )
| A. | y2=2$\sqrt{3}$x | B. | y2=4$\sqrt{3}$x | C. | y2=4x | D. | y2=6x |
8.如图的程序框图中输出S的结果是25,则菱形判断框内应填入的条件是( )


| A. | i<9 | B. | i≤9 | C. | i>9 | D. | i≥9 |
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线的方程为y=-$\sqrt{2}$x,则该双曲线的离心率为( )
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | 3 | D. | $\sqrt{3}$ |