题目内容
17.定义在R上的函数f(x)满足:f'(x)-f(x)>1,且f(0)=3,则不等式f(x)>4ex-1(其中e为自然对数的底数)的解集为(0,+∞).分析 设g(x)=e-xf(x)+e-x,利用导数性质得y=g(x)在定义域上单调递增,从而得到g(x)>g(0),由此能求出f(x)>4•ex-1(其中e为自然对数的底数)的解集
解答 解:设g(x)=e-xf(x)+e-x,
则g′(x)=-e-xf(x)+e-xf′(x)-e-x=e-x[f'(x)-f(x)-1],
∵f(x)-f′(x)>1,∴f(x)-f′(x)-1>0,
∴g′(x)>0,
∴y=g(x)在定义域上单调递增,g(0)=4,
∵f(x)>4•ex-1,∴e-xf(x)>4-e-x,得到g(x)>4=g(0),
∴g(x)>g(0).∴x>0,
∴f(x)>4•ex-1(其中e为自然对数的底数)的解集为(0,+∞).
故答案为:(0,+∞).
点评 本题考查函数的解集的求法;关键是利用已知条件适当构造新函数,利用函数的单调性求不等式的解集.

练习册系列答案
相关题目
5.下列命题正确的是( )
| A. | 若非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反,则$\overrightarrow{a}$+$\overrightarrow{b}$的方向必与$\overrightarrow{a}$,$\overrightarrow{b}$之一方向相同 | |
| B. | 在△ABC中,必有$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$ | |
| C. | 若$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$,则A,B,C为一个三角形的三个顶点 | |
| D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$为非零向量,则|$\overrightarrow{a}$+$\overrightarrow{b}$|与|$\overrightarrow{a}$|+|$\overrightarrow{b}$|一定相等 |
12.执行如图所示的程序框图,输出的结果是( )


| A. | 65 | B. | 45 | C. | 55 | D. | 34 |
2.若三点A(2,2),B(a,0),C(0,b)共线(a>0,b>0),则a+2b的最小值为( )
| A. | 12 | B. | 8$\sqrt{2}$ | C. | 6-4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
6.f:x→x2是集合A到集合B的映射,如果B={1,2},那么A∩B只可能是( )
| A. | {1,2} | B. | {1}或∅ | C. | $\left\{{1,\sqrt{2},2}\right\}$ | D. | {1} |
7.函数f(x)=x3-3|x|+1(x≤1)的零点所在区间为( )
| A. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{2},1)$ | B. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{3},\frac{1}{2})$ | C. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{2},1)$ | D. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{3},\frac{1}{2})$ |
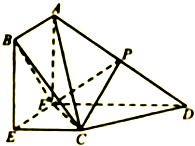 如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.
如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.