Question

求经过点A(-2,-4)且与直线l:x+3y=26相切于点B(8,6)的圆的方程.

Answer 1

思路分析:本题利用待定系数法求圆的方程及直线与圆的位置关系.若选用圆的标准方程,注意到圆的切线的性质,求出圆心坐标及半径;若采用圆的一般方程,则通过待定系数法求D、E、F.

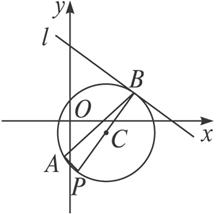
图4-2-8

解法一:设圆心为C(a,b),圆的方程为(x-a)²+(y-b)²=r².

再由|CA|=|CB|,CB⊥l可得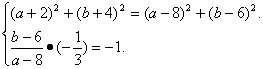

解得a=,b=,r=.故所求圆的方程为(x-)²+(y+)²=.

解法二:设圆心为C,则CB⊥l.

故直线CB的方程为3x-y-18=0.

设直线CB与圆C的另一交点为P,连结AP、AB,则AP⊥AB.

直线AP的斜率为-1,直线AP的方程为x+y+6=0.

由上述两个方程,可得P点坐标为(3,-9),

而C为线段BP的中点,

所以C点的坐标为(,).圆的半径为|CB|=.

因此,所求圆的方程为(x-)²+(y+)²=.

解法三:设圆的方程为x²+y²+Dx+Ey+F=0,

由CB⊥l,A(-2,-4)、B(8,6)在圆上,

所以得方程组

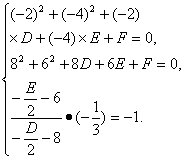
整理得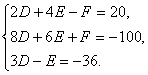

解得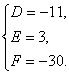故所求圆的方程为x²+y²-11x+3y-30=0.

  绿色通道:求圆的方程,一般可从圆的标准方程与圆的一般方程入手,至于选择哪一种方程形式更恰当,这要根据题目所给的条件来确定.总之,要让所选择的方程形式使解题过程简单.