题目内容
12．计算：C${\;}_{3}^{1}$+${C}_{4}^{2}$+${C}_{5}^{3}$+…+${C}_{99}^{97}$．分析 根据组合数的公式${C}_{n+1}^{m}={C}_{n}^{m}+{C}_{n}^{m-1}$，进行计算即可．
解答 解：C${\;}_{3}^{1}$+${C}_{4}^{2}$+${C}_{5}^{3}$+…+${C}_{99}^{97}$=${C}_{3}^{2}+{C}_{4}^{2}+{C}_{5}^{2}+{C}_{6}^{2}+…+{C}_{99}^{2}$
=（${C}_{3}^{3}$+C32）+C42+C52+…+C992-${C}_{3}^{3}$
=（${C}_{4}^{3}$+C42）+C52+…+C992-1
=（${C}_{5}^{3}$+C52）+…+C992-1
=…=${C}_{99}^{3}$+C992-1
=${C}_{100}^{3}$-1=161699．
点评 本题考查了利用组合数公式进行化简、计算的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
4．《张丘建算经》卷上第22题为：“今有女善织，日益功疾（注：第2天开始，每天比前天多织相同量的布），第一天织5尺布，现在一月（按30天计），共织390尺布”，则该女第5天所织的布的尺数为（ ）
| A． | 7 | B． | $\frac{107}{15}$ | C． | $\frac{219}{31}$ | D． | $\frac{209}{29}$ |
4．
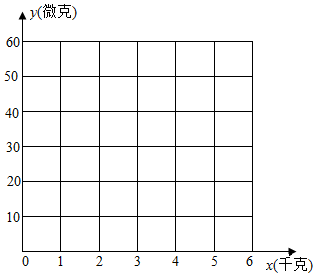菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，使用时需要用清水清洗干净，如表是用清水x（单位：千克）清洗该蔬菜1千克后，蔬菜上残留的农药y（单位：微克）的统计表：
（Ⅰ）在如图的坐标系中，描出散点图，并判断变量x与y的相关性；
（Ⅱ）若用解析式$\widehat{y}$=cx2+d作为蔬菜农药残量$\widehat{y}$与用水量x的回归方程，令ω=x2，计算平均值$\overline{ω}$和$\overline{y}$，完成如下表格，求出$\widehat{y}$与x回归方程．（c，d精确到0.01）
（Ⅲ）对于某种残留在蔬菜上的农药，当它的残留量低于20微克时对人体无害，为了放心食用该蔬菜，请估计需要多少千克的清水洗一千克蔬菜？（精确到0.1，参考数据$\sqrt{5}$≈2.236）．
（附：线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为：
$\widehat{b}$=$\frac{\sum_{i-1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．）
菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，使用时需要用清水清洗干净，如表是用清水x（单位：千克）清洗该蔬菜1千克后，蔬菜上残留的农药y（单位：微克）的统计表：| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
（Ⅱ）若用解析式$\widehat{y}$=cx2+d作为蔬菜农药残量$\widehat{y}$与用水量x的回归方程，令ω=x2，计算平均值$\overline{ω}$和$\overline{y}$，完成如下表格，求出$\widehat{y}$与x回归方程．（c，d精确到0.01）
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ωi-$\overline{ω}$ | |||||
| yi-$\overline{y}$ |
（附：线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为：
$\widehat{b}$=$\frac{\sum_{i-1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．）