题目内容
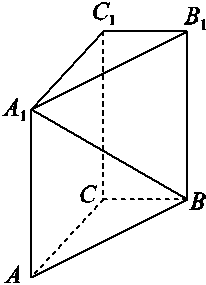
如图,底面为直角梯形的四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,E为A1B1的中点,且△ABE为等腰直角三角形,AB∥CD,AB⊥BC,AB=2CD=2BC.
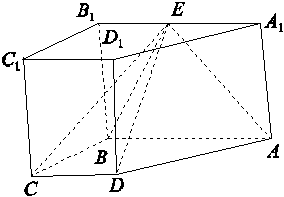
(1)求证:AB⊥DE;
(2)求直线EC与平面ABE所成角的正弦值;
(3)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出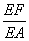 ;若不存在,请说明理由.
;若不存在,请说明理由.
解:(1)证明:取AB中点O,连接EO,DO.
因为EB=EA,所以EO⊥AB.
因为四边形ABCD为直角梯形,
AB=2CD=2BC,AB⊥BC,
所以四边形OBCD为正方形,
所以AB⊥OD.
又EO,OD为平面EOD内的两条相交直线,
所以AB⊥平面EOD.
因为ED⊂平面EOD,
所以AB⊥ED.
(2)因为AA1⊥平面ABCD,且EO∥AA1,
所以EO⊥平面ABCD,所以EO⊥OD.
由OD,OA,OE两两垂直,建立如图所示的空间直角坐标系O-xyz.
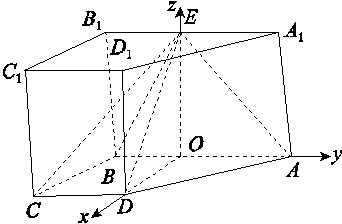
因为△EAB为等腰直角三角形,
所以OA=OB=OD=OE,设OB=1,
则O(0,0,0),A(0,1,0),B(0,-1,0),C(1,-1,0),D(1,0,0),E(0,0,1).
所以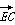 =(1,-1,-1),平面ABE的一个法向量为
=(1,-1,-1),平面ABE的一个法向量为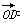 =(1,0,0).
=(1,0,0).
设直线EC与平面ABE所成的角为θ,
所以sin θ=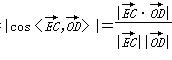 =
=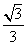 ,
,
即直线EC与平面ABE所成角的正弦值为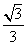 .
.
(3)存在点F,且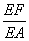 =
=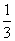 时,有EC∥平面FBD.证明如下:
时,有EC∥平面FBD.证明如下:
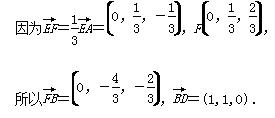 设平面FBD的法向量为ν=(a,b,c),
设平面FBD的法向量为ν=(a,b,c),
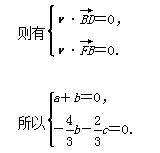 取a=1,
取a=1,
得ν=(1,-1,2).
因为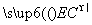 ·ν=(1,-1,-1)·(1,-1,2)=0,
·ν=(1,-1,-1)·(1,-1,2)=0,
即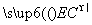 ⊥ν;
⊥ν;
又因为EC⊄平面FBD,
所以EC∥平面FBD.
因此当点F满足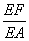 =
=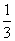 时,有EC∥平面FBD.
时,有EC∥平面FBD.

练习册系列答案
相关题目
 是(-∞,+∞)上的减函数,那么实数a的取值范围是( )
是(-∞,+∞)上的减函数,那么实数a的取值范围是( )
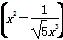 5的展开式中的常数项为T,f(x)是以T为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是________.
5的展开式中的常数项为T,f(x)是以T为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是________. 的零点个数为( )
的零点个数为( )