题目内容
已知点P(3,-4)是双曲线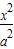 -
-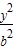 =1(a>0,b>0)渐近线上的一点,E,F是左、右两个焦点,若
=1(a>0,b>0)渐近线上的一点,E,F是左、右两个焦点,若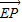 •
•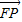 =0,则双曲线方程为( )
=0,则双曲线方程为( )A.
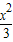 -
-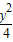 =1
=1B.
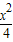 -
-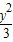 =1
=1C.
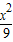 -
-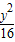 =1
=1D.
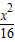 -
-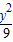 =1
=1
【答案】分析:根据题意,设E、F的坐标为E(-c,0),F(c,0),又由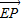 •
•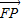 =0,结合数量积的坐标运算,可得c的值,进而由P坐标与双曲线的定义2a=||PE|-|PF||,可得a的值,根据则b=
=0,结合数量积的坐标运算,可得c的值,进而由P坐标与双曲线的定义2a=||PE|-|PF||,可得a的值,根据则b=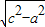 ,可得b的值,将a、b的值代入可得双曲线的方程.
,可得b的值,将a、b的值代入可得双曲线的方程.
解答:解:设E(-c,0),F(c,0),
于是有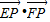 =(3+c,-4)•(3-c,-4)=9-c2+16=0.
=(3+c,-4)•(3-c,-4)=9-c2+16=0.
于是c2=25,
则E(-5,0),F(5,0),
由双曲线的定义,可得2a=||PE|-|PF||=6,
则a=3;
则b=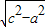 =4;
=4;
故双曲线方程为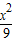 -
-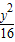 =1;
=1;
故选C.
点评:本题考查双曲线的标准方程,解题时结合双曲线的定义,并注意区分双曲线与椭圆定义的区别.
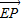 •
•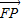 =0,结合数量积的坐标运算,可得c的值,进而由P坐标与双曲线的定义2a=||PE|-|PF||,可得a的值,根据则b=
=0,结合数量积的坐标运算,可得c的值,进而由P坐标与双曲线的定义2a=||PE|-|PF||,可得a的值,根据则b=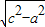 ,可得b的值,将a、b的值代入可得双曲线的方程.
,可得b的值,将a、b的值代入可得双曲线的方程.解答:解:设E(-c,0),F(c,0),
于是有
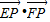 =(3+c,-4)•(3-c,-4)=9-c2+16=0.
=(3+c,-4)•(3-c,-4)=9-c2+16=0.于是c2=25,
则E(-5,0),F(5,0),
由双曲线的定义,可得2a=||PE|-|PF||=6,
则a=3;
则b=
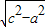 =4;
=4;故双曲线方程为
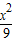 -
-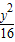 =1;
=1;故选C.
点评:本题考查双曲线的标准方程,解题时结合双曲线的定义,并注意区分双曲线与椭圆定义的区别.

练习册系列答案
相关题目
已知点P(3,-4)是双曲线
-
=1(a>0,b>0)渐近线上的一点,E,F是左、右两个焦点,若
•
=0,则双曲线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| EP |
| FP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|