题目内容
10.判断函数f(x)=$\frac{1}{{x}^{2}-2x-3}$的单调性.分析 可令x2-2x-3=t,(-4≤t<0,或t>0),设y=f(x),从而得到y=$\frac{1}{t}$,可判断二次函数t=x2-2x-3在(-∞,-1),(-1,1)上单调递减,而在(1,3),(3,+∞)上单调递增,这样根据复合函数的单调性的判断即可得出f(x)的单调性.
解答 解:令x2-2x-3=t,-4≤t<0,或t>0,设y=f(x),则:
$y=\frac{1}{t}$,在t∈[-4,0),(0,+∞)上单调递减;
x∈(-1,3)时,t<0,x∈(-∞,-1)∪((3,+∞)时,t>0;
函数t=x2-2x-3的对称轴为x=1,该函数在(-1,1),(-∞,-1)单调递减,在(1,3),(3,+∞)上单调递增;
∴根据复合函数的单调性得,f(x)在(-1,1),(-∞,-1)上单调递增,在(1,3),(3,+∞)上单调递减.
点评 考查复合函数单调性的判断,二次函数的对称轴,二次函数单调性的判断,以及反比例函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.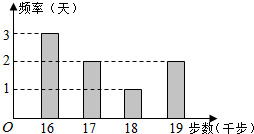 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.
 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:| 健步走步数(前步) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.
1.阅读如图所示的程序框图,若输入的k=10,那么输出的S值为( )


| A. | 1024 | B. | 2036 | C. | 1023 | D. | 511 |
20.已知圆M上有三点,A(1,0),B(0,$\sqrt{3}$),C(2,$\sqrt{3}$),则直线x-$\sqrt{3}$y+1=0被圆M截得的弦长为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{21}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
 已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,交半圆于点E,DE=1
已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,交半圆于点E,DE=1