��Ŀ����
����Ŀ����ͼ��һ��Բ�Ľ�Ϊֱ�ǵ�����AOB ���ݷ����뾶Ϊ1����P �ǻ��ݷ�����һ�����㣬�����˵㣬�ִ���������BOP ���ֻ���PQ��OA������ΪQ��PQ ������AOP �ֳ����������֣���PQ ��ಿ��������POQ Ϊ����������PQ �Ҳಿ���ֲݣ���֪�ֻ��ĵ�λ��������Ϊ3a���ֲݵĵ�λ��������Ϊ2a������a Ϊ�����������AOP=�ȣ��ֻ���������ֲݵ���۵ĺͳ�Ϊ����ۣ����ƹ���������ۣ��������Ϊf���ȣ� 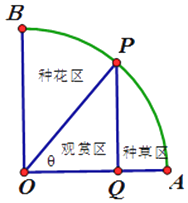
��1����f���ȣ����ڦ� �ĺ�����ϵʽ��
��2���� Ϊ��ֵʱ���������С���������Сֵ��
���𰸡�
��1���⣺�ֻ��������Ϊ ![]() ���ֲ��������Ϊ
���ֲ��������Ϊ ![]() ��
��
�������f���ȣ�= ![]() ��
�� ![]() ���ȣ�+��
���ȣ�+�� ![]() ��
�� ![]() sin��cos�ȣ�2��=��
sin��cos�ȣ�2��=�� ![]() ��
�� ![]() ��sin��cos�ȣ�����0���ȣ�
��sin��cos�ȣ�����0���ȣ� ![]()
��2���⣺ ![]() =
= ![]()
��f'���ȣ�=0���õ� ![]()
�� | | | |
f'���ȣ� | _ | 0 | + |
f���ȣ� | �ݼ� | ��Сֵ | ���� |
�ʵ� ![]() ʱ���������С�����������СΪ
ʱ���������С�����������СΪ 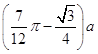
����������1���ֱ�����ֻ�������ۣ��ֲ�������ۣ����ɵõ�f���ȣ����ڦ� �ĺ�����ϵʽ����2�������ٸ��ݵ����ͺ�������ֵ�ù�ϵ��������𰸣�
�����㾫�������ڱ��⿼������������ʽ����Ҫ�˽������ε�Բ�Ľ�Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() ������Ϊ
������Ϊ![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ���ܵó���ȷ�𰸣�
���ܵó���ȷ�𰸣�

 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�