Question

【题目】以直角坐标系原点O为极点，x轴正方向为极轴，已知曲线C1的参数方程为 （t为参数），C2的极坐标方程为ρ2（1+sin2θ）=8，C3的极坐标方程为θ=α，α∈[0，π），ρ∈R，
（1）若C1与C3的一个公共点为A（异于O点），且|OA|= ，求α；
（2）若C1与C3的一个公共点为A（异于O点），C2与C3的一个公共点为B，求|OA||OB|的取值范围．

Answer 1

【答案】
（1）解：曲线C1的参数方程为 （t为参数），则直角方程为（x﹣1）2+y2=1，

极坐标方程为ρ=2cosθ，联立极坐标方程 ，得 ，

由|OA|= =丨ρ1﹣ρ2丨=丨2cosα丨，

解得cosα=± ，则α= 或α= ．

（2）解：联立C1与C3的极坐标方程为 ，丨OB丨=丨ρ丨= ，

当α= 时，O与A重合，所以α≠ ，则

|OA||OB|=丨2cosα丨 =4 =4 =4 ，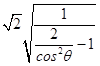

∴|OA||OB|∈（0，4 ]，

|OA||OB|的取值范围∈（0，4 ]．

【解析】（1）由曲线C1的参数方程求得直角坐标方程，即可求得极坐标方程，与曲线C3联立，即可求得ρ1，ρ2，由|OA|=丨ρ1﹣ρ2丨，即可求得α；（2）联立C1与C3的极坐标方程．即可求得丨OB丨，则|OA||OB|=丨2cosα丨 ，化简即可求得|OA||OB|的取值范围．