题目内容
【题目】设数列{an}是公差大于0的等差数列，Sn为数列{an}的前n项和，已知S3=9，且2a1 ， a3﹣1，a4+1构成等比数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足 
=2n﹣1（n∈N*），设Tn是数列{bn}的前n项和，证明：Tn＜6．
【答案】
（1）解：∵公差不为零的等差数列{an}的前3项和S3=9，得到a2=3，
且2a1，a3﹣1，a4+1构成等比数列，
∴得到未知数a2与d的方程组：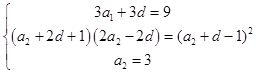 
，
由d≠0，解得a1=1，d=2，
∴an=2n﹣1．
（2）证明：∵数列{bn}满足 
=2n﹣1（n∈N*），
∴ 
，∴bn=（2n﹣1）21﹣n=（4n﹣2） 
设Tn是数列{bn}的前n项和，
则Tn=2 
+6 
+10 
+14 
+…+（4n﹣2） ，①
=2 +6 
…+（4n﹣2） 
，②
①﹣②，得： Tn=1+1+ 
﹣ 
=1+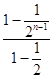 
﹣（4n﹣2） 
=3﹣ 
，
∴Tn=6﹣ 
＜6．
∴Tn＜6．
【解析】（1）利用等差数列前n项和、通项公式和等比数列，列出方程组，求出首项与公差，由此能求出数列{an}的通项公式．（2）推导出bn=（2n﹣1）21﹣n=（4n﹣2） 
利用错位相减法求出数列{bn}的前n项和，由此能证明Tn＜6．
【考点精析】关于本题考查的数列的前n项和和数列的通项公式，需要了解数列{an}的前n项和sn与通项an的关系
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公就叫这个数列的通项公式才能得出正确答案．
练习册系列答案
相关题目
