��Ŀ����
6��ij���Ҿ��д��͵Ĵ������������ij��Ʒ����������Ϊx��Ԫʱ��������t�������t=5-$\frac{9}{2��x+1��}$������0��x��a��aΪ�����������ּٶ�����������������ȣ���֪�����ò�Ʒt�������Ͷ��ɱ���10+2t����Ԫ�������������ã�����Ʒ�����ۼ۸�Ϊ��4+$\frac{20}{t}$����Ԫ/�������I�����ò�Ʒ������y��Ԫ��ʾΪ��������x��Ԫ�ĺ�����
��II����������Ͷ�������Ԫʱ�����ҵ��������
���� ����ȷ���ò�Ʒ�ۼ�Ϊ��4+$\frac{20}{t}$����Ԫ��y=t����4+$\frac{20}{t}$��-��10+2t��-x��������t�������t=5-$\frac{9}{2��x+1��}$�����뻯��øò�Ʒ������y��Ԫ��ʾΪ��������x��Ԫ�ĺ�����
���������ۣ����û�������ʽ�������ĵ����ԣ����ҵ��������
��� �⣺����������֪������y=t����4+$\frac{20}{t}$��-��10+2t��-x
��������t�������t=5-$\frac{9}{2��x+1��}$������0��x��a��a����������
���뻯��ɵã�y=20-��$\frac{9}{x+1}$+x������0��x��a��aΪ��������
����y=21-��$\frac{9}{x+1}$+x+1����21-6=15��
���ҽ���$\frac{9}{x+1}$=x+1����x=2ʱ����ʽȡ�Ⱥţ�
��a��2ʱ����������Ͷ��2��Ԫʱ�����ҵ��������
��0��a��2ʱ��y��0��x��a�ϵ���������
x=a�����������ֵ����������Ͷ��x=a��Ԫʱ�����ҵ��������
����������a��2ʱ����������Ͷ��2��Ԫʱ�����ҵ��������
��0��a��2ʱ����������Ͷ��x=a��Ԫʱ�����ҵ��������
���� ���⿼�麯��ģ�͵�ѡ����Ӧ�ã������������ʽ�����ã�ȷ����������ʽ�ǹؼ���

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�| A�� | -2 011 | B�� | -2 012 | C�� | -2 010 | D�� | -2 013 |
| A�� | -3 | B�� | -2 | C�� | 0 | D�� | 1 |
| A�� | 1+i | B�� | 1-i | C�� | 1+$\frac{i}{2}$ | D�� | 1-$\frac{i}{2}$ |
| A�� | $��-�ޣ�-\sqrt{2}��$ | B�� | $��-�ޣ�-\frac{{\sqrt{2}}}{2}��$ | C�� | $��-\sqrt{2}��\frac{{\sqrt{2}}}{2}��$ | D�� | $��-�ޣ�\sqrt{2}��$ |
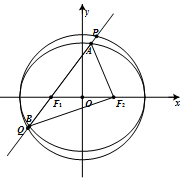 ��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����ԲO��x2+y2=a2��F1��-1��0����F2��1��0���ֱ�����Բ�����������㣬��F1����б��Ϊ��$��{���ʣ�{0��\frac{��}{2}}]}��$�Ķ�ֱ��l����ԲC��A��B���㣬��ԲO��P��Q���㣨��ͼ��ʾ����A��x���Ϸ���������=$\frac{��}{4}$ʱ����PQ�ij�Ϊ$\sqrt{14}$��
��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����ԲO��x2+y2=a2��F1��-1��0����F2��1��0���ֱ�����Բ�����������㣬��F1����б��Ϊ��$��{���ʣ�{0��\frac{��}{2}}]}��$�Ķ�ֱ��l����ԲC��A��B���㣬��ԲO��P��Q���㣨��ͼ��ʾ����A��x���Ϸ���������=$\frac{��}{4}$ʱ����PQ�ij�Ϊ$\sqrt{14}$�� 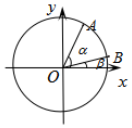 ��ͼ����ƽ��ֱ������ϵxOy�У���x��Ϊʼ����������Ǧ����£����ǵ��ձ߷ֱ��뵥λԲ����A��B���㣮��֪$A��\frac{{\sqrt{5}}}{5}��\;\frac{{2\sqrt{5}}}{5}��\;��\;\;B��\frac{{7\sqrt{2}}}{10}��\;\frac{{\sqrt{2}}}{10}��$
��ͼ����ƽ��ֱ������ϵxOy�У���x��Ϊʼ����������Ǧ����£����ǵ��ձ߷ֱ��뵥λԲ����A��B���㣮��֪$A��\frac{{\sqrt{5}}}{5}��\;\frac{{2\sqrt{5}}}{5}��\;��\;\;B��\frac{{7\sqrt{2}}}{10}��\;\frac{{\sqrt{2}}}{10}��$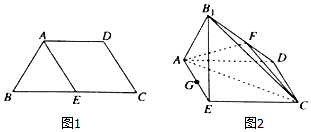 ��֪�ı���ABCD����AD��BC��BA=AD=DC=$\frac{1}{2}$BC=a��E��BC���е㣬����BAE����AE���۳ɡ�B1AE��ʹƽ��B1AE��ƽ��ABCD��F��G�ֱ�ΪB1D��AE���е㣮
��֪�ı���ABCD����AD��BC��BA=AD=DC=$\frac{1}{2}$BC=a��E��BC���е㣬����BAE����AE���۳ɡ�B1AE��ʹƽ��B1AE��ƽ��ABCD��F��G�ֱ�ΪB1D��AE���е㣮