题目内容
2.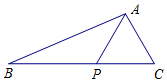 如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.
如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.(Ⅰ) 求∠ACP;
(Ⅱ) 若△APB的面积是$\frac{{3\sqrt{3}}}{2}$,求sin∠BAP.
分析 (Ⅰ) 在△APC中,由余弦定理得AP2-4AP+4=0,解得AP=2,可得△APC是等边三角形,即可得解.
(Ⅱ) 法1:由已知可求∠APB=120°.利用三角形面积公式可求PB=3.进而利用余弦定理可求AB,在△APB中,由正弦定理可求sin∠BAP=$\frac{{3sin{{120}°}}}{{\sqrt{19}}}$的值.
法2:作AD⊥BC,垂足为D,可求:$PD=1,AD=\sqrt{3},∠PAD={30°}$,利用三角形面积公式可求PB,进而可求BD,AB,利用三角函数的定义可求$sin∠BAD=\frac{BD}{AB}=\frac{4}{{\sqrt{19}}}$,$cos∠BAD=\frac{AD}{AB}=\frac{{\sqrt{3}}}{{\sqrt{19}}}$.利用两角差的正弦函数公式可求sin∠BAP=sin(∠BAD-30°)的值.
解答  (本题满分为12分)
(本题满分为12分)
解:(Ⅰ) 在△APC中,因为∠PAC=60°,PC=2,AP+AC=4,
由余弦定理得PC2=AP2+AC2-2•AP•AC•cos∠PAC,…(1分)
所以22=AP2+(4-AP)2-2•AP•(4-AP)•cos60°,
整理得AP2-4AP+4=0,…(2分)
解得AP=2.…(3分)
所以AC=2.…(4分)
所以△APC是等边三角形.…(5分)
所以∠ACP=60°.…(6分)
(Ⅱ) 法1:由于∠APB是△APC的外角,所以∠APB=120°.…(7分)
因为△APB的面积是$\frac{{3\sqrt{3}}}{2}$,所以$\frac{1}{2}•AP•PB•sin∠APB=\frac{{3\sqrt{3}}}{2}$.…(8分)
所以PB=3.…(9分)
在△APB中,AB2=AP2+PB2-2•AP•PB•cos∠APB=22+32-2×2×3×cos120°=19,
所以$AB=\sqrt{19}$.…(10分)
在△APB中,由正弦定理得$\frac{AB}{sin∠APB}=\frac{PB}{sin∠BAP}$,…(11分) 所以sin∠BAP=$\frac{{3sin{{120}°}}}{{\sqrt{19}}}$=$\frac{{3\sqrt{57}}}{38}$.…(12分)
所以sin∠BAP=$\frac{{3sin{{120}°}}}{{\sqrt{19}}}$=$\frac{{3\sqrt{57}}}{38}$.…(12分)
法2:作AD⊥BC,垂足为D,
因为△APC是边长为2的等边三角形,
所以$PD=1,AD=\sqrt{3},∠PAD={30°}$.…(7分)
因为△APB的面积是$\frac{{3\sqrt{3}}}{2}$,所以$\frac{1}{2}•AD•PB=\frac{{3\sqrt{3}}}{2}$.…(8分)
所以PB=3.…(9分)
所以BD=4.
在Rt△ADB中,$AB=\sqrt{B{D^2}+A{D^2}}=\sqrt{19}$,…(10分)
所以$sin∠BAD=\frac{BD}{AB}=\frac{4}{{\sqrt{19}}}$,$cos∠BAD=\frac{AD}{AB}=\frac{{\sqrt{3}}}{{\sqrt{19}}}$.
所以sin∠BAP=sin(∠BAD-30°)=sin∠BADcos30°-cos∠BADsin30°…(11分)
=$\frac{4}{{\sqrt{19}}}×\frac{{\sqrt{3}}}{2}-\frac{{\sqrt{3}}}{{\sqrt{19}}}×\frac{1}{2}$=$\frac{{3\sqrt{57}}}{38}$.…(12分)
点评 本题主要考查了余弦定理,三角形面积公式,正弦定理,三角函数的定义,两角差的正弦函数公式在解三角形中的应用,考查了计算能力和数形结合思想,考查了转化思想,属于中档题.

| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | -1 | D. | 2 |
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{30}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
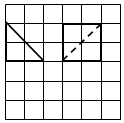 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为$\frac{8}{3}$,则该几何体的俯视图可以是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为$\frac{8}{3}$,则该几何体的俯视图可以是( )