题目内容
已知函数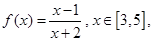
⑴ 判断函数 的单调性,并证明;
的单调性,并证明;
⑵ 求函数 的最大值和最小值
的最大值和最小值
⑴详见解析;⑵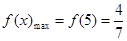 ,
,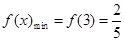
解析试题分析:⑴用单调性的定义证明:在定义域内任取两个数并规定其大小关系,用作差法判断两个函数值的大小,若自变量大对应的函数值也大,说明函数在此区间上单调递增,否则单调递减。⑵用单调性求最值。
试题解析:解:⑴ 设任取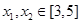 且
且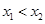



 即
即
 在
在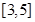 上为增函数
上为增函数
⑵ 由⑴知 在
在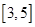 上单调递增,
上单调递增,
所以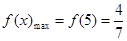
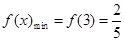
考点:1单调性的定义;2用单调性求最值。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 ,若函数
,若函数 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数 的取值范围.
的取值范围. ;
; ;
; (k∈R,且k>0).
(k∈R,且k>0).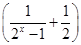 x3.
x3. ,
,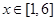 ,
, .
. ,试判断并证明函数
,试判断并证明函数 的单调性;
的单调性;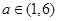 时,求函数
时,求函数 .
. .
.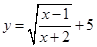 .
. 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.