题目内容
已知函数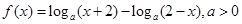 且
且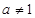 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性并予以证明.
的奇偶性并予以证明.
(1) ;(2)奇函数,证明详见解析.
;(2)奇函数,证明详见解析.
解析试题分析:(1)根据对数函数的真数大于0,求解不等式 即可得到函数
即可得到函数 的定义域;(2)从奇偶函数的定义上进行判断、证明该函数的奇偶性,即先由(1)说明函数的定义域关于原点对称;然后求出
的定义域;(2)从奇偶函数的定义上进行判断、证明该函数的奇偶性,即先由(1)说明函数的定义域关于原点对称;然后求出 ,若
,若 ,则该函数为偶函数,若
,则该函数为偶函数,若 ,则该函数的奇函数.
,则该函数的奇函数.
试题解析:(1)由题得 3分
3分
所以函数 的定义域为
的定义域为 5分
5分
(2)函数 为奇函数 6分
为奇函数 6分
证明:由(1)知函数 的定义域关于原点对称 7分
的定义域关于原点对称 7分
且

所以函数 为奇函数 10分.
为奇函数 10分.
考点:1.对数函数的图像与性质;2.函数的奇偶性.

练习册系列答案
相关题目
 ;
; ;
; ,
,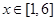 ,
, .
. ,试判断并证明函数
,试判断并证明函数 的单调性;
的单调性;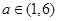 时,求函数
时,求函数 .
. +2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
+2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.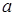 为正实数,函数
为正实数,函数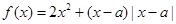 .
.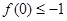 ,求
,求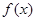 的最小值;
的最小值;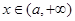 ,求不等式
,求不等式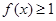 的解集.
的解集. 且
且 的图象经过点
的图象经过点 .
.  的解析式;
的解析式; ,用函数单调性的定义证明:函数
,用函数单调性的定义证明:函数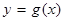 在区间
在区间 上单调递减;
上单调递减; .
. .
.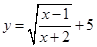 .
.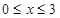 时,f(x)=
时,f(x)=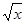 -1.
-1.