题目内容
19.设等差数列{an}满足a1=-11,a4+a6=-6,(1)求{an}的通项公式an;
(2)设{an}的前n项和为Sn,求满足sk=189成立的k值.
分析 (1)利用等差数列的通项公式即可得出.
(2)利用(1)中该数列的通项公式,易得sk=k2-12k=189,通过解该方程求得k的值即可.
解答 解:(1)设等差数列{an}的公差为d,
∵a1=-11,a4+a6=-6,
∴2×(-11)+8d=-6,
解得d=2.
∴an=-11+2(n-1)=2n-13.
(2)由(1)得${s_n}={n^2}-12n$.
由sk=189得k2-12k=189,
解得k=21,k=-9(舍),
∴k=21.
点评 本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.已知函数f(x)=$\sqrt{{x}^{2}-2ax+3}$在(-1,1)上是单调递增的,则a的取值范围是( )
| A. | [-2,-1] | B. | (-∞,-1] | C. | [1,2] | D. | [1,+∞) |
14.某高校调查询问了56名男女大学生在课余时间是否参加运动,得到下表所示的数据.从表中数据分析,有多大把握认为大学生的性别与参加运动之间有关系.
| 参加运动 | 不参加运动 | 合计 | |
| 男大学生 | 20 | 8 | 28 |
| 女大学生 | 12 | 16 | 28 |
| 合计 | 32 | 24 | 56 |
4.下列说法中正确的是( )
| A. | 任一事件的概率总在(0,1)内 | B. | 不可能事件的概率不一定为0 | ||
| C. | 必然事件的概率一定为1 | D. | 概率为0的事件一定是不可能事件 |
8.若sin(π-α)=-$\frac{{\sqrt{3}}}{3}$,且α∈(π,$\frac{3π}{2}$),则sin($\frac{π}{2}$+α)=( )
| A. | -$\frac{\sqrt{6}}{3}$ | B. | -$\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
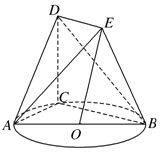 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3