题目内容
12.若(2+x)(1-x)6=a0+a1x+a2x2+…+a7x7,则a2+a3=-1.分析 根据题意只要先求出(1-x)6的通项,求解展开式中的含x2,x3项的系数,即可求a2,a3,从而得解a2+a3的值.
解答 解:由于:(2+x)(1-x)6=a0+a1x+a2x2+…+a7x7,
而:(1-x)6展开式的通项为:Tr+1=C${\;}_{6}^{r}$(-x)r,
所以:(2+x)(1-x)6展开式中含x2的项为:2C${\;}_{6}^{2}$(-x)2+x•C${\;}_{6}^{1}$(-x)=30x2-6x2=24x2,可得:a2=24,
(2+x)(1-x)6展开式中含x3的项为:2C${\;}_{6}^{3}$(-x)3+x•C${\;}_{6}^{2}$(-x)2=-40x3+15x3=-25x3,可得:a3=-25,
∴a2+a3=-1.
故答案为:-1.
点评 本题主要考查了二项展开式的通项在求解指定项中的应用,解题的关键是寻求指定项得到的途径,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知函数f(x)=2ax3-3ax2+1,g(x)=-$\frac{a}{4}x+\frac{3}{2}$,若对任意给定的m∈[0,2],关于x的方程f(x)=g(m)在区间[0,2]上总存在两个不同的解,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | [-1,1] |
20.阅读如图的程序框图,运行相应的程序,则输出的值为( )


| A. | 81 | B. | 27 | C. | 16 | D. | 9 |
7.根据表格中的数据用最小二乘法计算出变量x、y的线性回归方程为$\stackrel{∧}{y}$=3x-$\frac{3}{2}$,则表格中m的值是( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | 8 | m |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
4.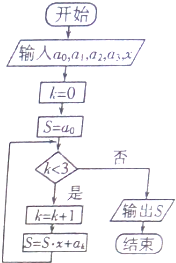 如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( )
如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( )
 如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( )
如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( )| A. | a0+a1+a2+a3 | B. | (a0+a1+a2+a3)x3 | ||
| C. | a0+a1x+a2x2+a3x3 | D. | a0x3+a1x2+a2x+a3 |