题目内容
设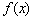 是定义在
是定义在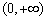 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记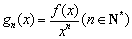 .若对定义域内的每一个
.若对定义域内的每一个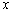 ,总有
,总有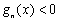 ,则称
,则称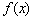 为“
为“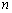 阶负函数”;若对定义域内的每一个
阶负函数”;若对定义域内的每一个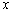 ,总有
,总有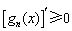 ,则称
,则称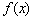 为“
为“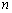 阶不减函数”(
阶不减函数”(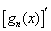 为函数
为函数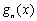 的导函数).
的导函数).
(1)若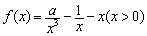 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数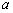 的取值范围;
的取值范围;
(2)对任给的“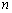 阶不减函数”
阶不减函数”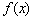 ,如果存在常数
,如果存在常数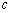 ,使得
,使得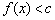 恒成立,试判断
恒成立,试判断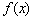 是否为“
是否为“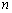 阶负函数”?并说明理由.
阶负函数”?并说明理由.
练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
题目内容
设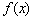 是定义在
是定义在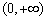 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记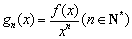 .若对定义域内的每一个
.若对定义域内的每一个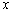 ,总有
,总有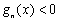 ,则称
,则称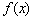 为“
为“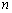 阶负函数”;若对定义域内的每一个
阶负函数”;若对定义域内的每一个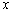 ,总有
,总有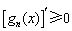 ,则称
,则称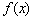 为“
为“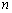 阶不减函数”(
阶不减函数”(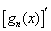 为函数
为函数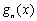 的导函数).
的导函数).
(1)若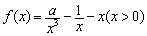 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数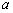 的取值范围;
的取值范围;
(2)对任给的“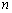 阶不减函数”
阶不减函数”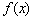 ,如果存在常数
,如果存在常数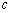 ,使得
,使得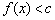 恒成立,试判断
恒成立,试判断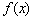 是否为“
是否为“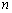 阶负函数”?并说明理由.
阶负函数”?并说明理由.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案