题目内容
已知正△ABC边长等于
,点P在其外接圆上运动,则
•
的最大值是 .
| 3 |
| PA |
| PB |
考点:向量的模
专题:数形结合,平面向量及应用
分析:结合图形,利用向量数量积公式把
•
化为三角函数形式,利用和差化积公式化为一个角的三角函数,根据三角函数的值域求得最大值.
| PA |
| PB |
解答:
解:如图所示.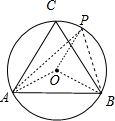
由正△ABC边长等于
,点P在其外接圆上运动.
∴∠AOB=120°,R=
×
=1.
∴
•
=(
-
)•(
-
)
=
•
-
•
-
•
+
2
=cos120°-cos∠POB-cos∠AOP+1
=
-2cos∠AOBcos(
)=
+cos(
),
∵cos(
)≤1,
∴当∠AOP=∠BOP时,
•
最大,且最大值为
.
故答案为:
.

由正△ABC边长等于
| 3 |
∴∠AOB=120°,R=
| 1 |
| 2 |
| ||
| sin60° |
∴
| PA |
| PB |
| OA |
| OP |
| OB |
| OP |
=
| OA |
| OB |
| OA |
| OP |
| OP |
| OB |
| OP |
=cos120°-cos∠POB-cos∠AOP+1
=
| 1 |
| 2 |
| ∠AOP-∠BOP |
| 2 |
| 1 |
| 2 |
| ∠AOP-∠BOP |
| 2 |
∵cos(
| ∠AOP-∠BOP |
| 2 |
∴当∠AOP=∠BOP时,
| PA |
| PB |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了向量的数量积公式,正弦定理及三角函数的和差化积公式,数形结合是解答本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
在△ABC中,内角A、B、C满足:sin2A+
sinAsinB+sin2B=sin2C,则∠C等于( )
| 2 |
| A、45° | B、135° |
| C、30° | D、150° |
曲线f(x)=xlnx+2在点x=1处的切线方程为( )
| A、y=2x+2 |
| B、y=2x-2 |
| C、y=x-1 |
| D、y=x+1 |
已知向量
=(3,1),
=(1,3),
=(k,7),若(
-
)∥
,则k=( )
| a |
| b |
| c |
| a |
| c |
| b |
| A、1 | B、3 | C、5 | D、7 |
如果执行如图的程序框图,输出的S=72,则判断框中为( )


| A、k≥9 | B、k≤8 |
| C、k≤9 | D、k≥8 |