题目内容
10. 为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.| 非手机迷 | 手机迷 | 合计 | |
| 男 | x | x | m |
| 女 | y | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)能否有95%的把握认为“手机控”与性别有关?
注:k2=$\frac{n(ac-bd)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(k2≥x0) | 0.05 | 0.10 |
| k0 | 3.841 | 6.635 |
分析 (1)由频率分布直方图能求出在抽取的100人中,“手机控”的人数.
(2)求出2×2列联表,假设H0:“手机控”与性别没有关系,求出K2<3.841,从而得到没有95%把握认为“手机控”与性别有关.
解答 解:(1)由频率分布直方图可知,在抽取的100人中,“手机控”有:100×(0.2+0.05)=25人,非手机控75人,∴x=30,y=45,m=15.n=45;
(2)从而2×2列联表如下:
| 非手机控 | 手机控 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
假设H0:“手机控”与性别没有关系.
将2×2列联表中的数据代入公式,计算得:K2=$\frac{100×(30×10-15×45)^{2}}{45×55×75×25}$≈3.030,
当H0成立时,P(K2≥3.841)≈0.05.
∴3.030<3.841,所以没有95%把握认为“手机控”与性别有关
点评 本题考查独立性检验的应用,考查学生的计算能力,是中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
5.一个几何体的三视图如图所示,则该几何体的体积为( )
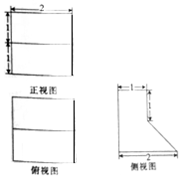

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
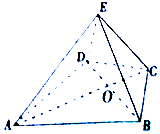 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.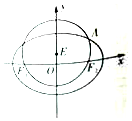 如图,在平面直角坐标系xOy中,已知圆E:x2+(y-t)2=r2(t>0,r>0)经过椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,在平面直角坐标系xOy中,已知圆E:x2+(y-t)2=r2(t>0,r>0)经过椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.