题目内容
20.对于二次函数y=-4x2+8x-3,(1)若x∈R
①指出图象的开口方向、对称轴方程、顶点坐标;
②求函数的最大值或最小值;
③分析函数的单调性.
(2)若x∈[-1,5),试确定y的取值范围.
分析 (1)①将二次函数配方,结合图象,可得开口方向、对称轴方程、顶点坐标;
②由顶点处取得最值,可得函数的最大值或最小值;
③结合图象和对称轴,可得单调性;
(2)考虑对称轴与区间的关系,判断单调性,即可得到所求范围.
解答 解:(1)①二次函数y=-4x2+8x-3,
即为y=-4(x-1)2+1,
函数图象的开口方向向下、对称轴方程为x=1、顶点坐标(1,1);
②当x=1时,函数的最大值为1,无最小值;
③函数f(x)在(-∞,1)递增,在(1,+∞)递减.
(2)x∈[-1,5),
f(x)在[-1,1)递增,在(1,5)递减,
可得f(1)取得最大值1,又f(-1)=-15,f(5)=-63.
则函数y的取值范围是(-63,1].
点评 本题考查二次函数的图象和性质,主要考查函数的最值和在闭区间上的值域,注意运用单调性,考虑对称轴和区间的关系,考查运算能力,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
10. 为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
(1)求列表中数据的值;
(2)能否有95%的把握认为“手机控”与性别有关?
注:k2=$\frac{n(ac-bd)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.| 非手机迷 | 手机迷 | 合计 | |
| 男 | x | x | m |
| 女 | y | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)能否有95%的把握认为“手机控”与性别有关?
注:k2=$\frac{n(ac-bd)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(k2≥x0) | 0.05 | 0.10 |
| k0 | 3.841 | 6.635 |
8.已知函数f(x)=2sin(ωx+φ)-1(ω>0,|φ|<π)的一个零点是$x=\frac{π}{3}$,$x=-\frac{π}{6}$是y=f(x)的图象的一条对称轴,则ω取最小值时,f(x)的单调增区间是( )
| A. | $[{-\frac{7}{3}π+3kπ,-\frac{1}{6}π+3kπ}],k∈Z$ | B. | $[{-\frac{5}{3}π+3kπ,-\frac{1}{6}π+3kπ}],k∈Z$ | ||
| C. | $[{-\frac{2}{3}π+2kπ,-\frac{1}{6}π+2kπ}],k∈Z$ | D. | $[{-\frac{1}{3}π+2kπ,-\frac{1}{6}π+2kπ}],k∈Z$ |
5.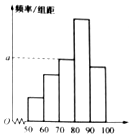 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
(1)求表中t,q及图中a的值;
(2)该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批,设X表示所抽取学生中成绩低于60分的人数,求随机变量X的分布列和数学期望.
 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
(2)该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批,设X表示所抽取学生中成绩低于60分的人数,求随机变量X的分布列和数学期望.
12.从4款甲型和5款乙型智能手机中任取3款,其中至少要甲乙型号各一款,则不同的取法共有( )
| A. | 140种 | B. | 80种 | C. | 70种 | D. | 35种 |
10.命题p:?x∈R,x≥0的否定是( )
| A. | ¬p:?x∈R,x<0 | B. | ¬p:?x∈R,x≤0 | C. | ¬p:?x∈R,x<0 | D. | ¬p:?x∈R,x≤0 |