题目内容
f（x）=lg（1-x2）值域为 ．
考点：对数函数的值域与最值
专题：函数的性质及应用
分析：判断出1-x2的范围，根据对数函数的单调性求得函数的值域．
解答：
解：∵x2≥0，
∴0＜1-x2≤1，
∵f（x）=lg（1-x2）为单调增函数，
∴lg（1-x2）≤0，即函数的值域为（-∞，0]，
故答案为：（-∞，0]．
∴0＜1-x2≤1，
∵f（x）=lg（1-x2）为单调增函数，
∴lg（1-x2）≤0，即函数的值域为（-∞，0]，
故答案为：（-∞，0]．
点评：本题主要考查了对数函数的值域问题．巧妙的利用函数的单调性来求得函数的值域．
练习册系列答案
相关题目
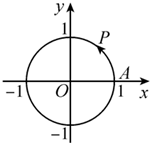如图，半径为1的圆的圆心位于坐标原点，点P从点A（1，0）出发，依逆时针方向等速沿单位圆周旋转．已知点P在1秒钟内转过的角度为θ（0＜θ＜π），经过2秒钟到达第三象限，经过14秒钟后又恰好回到出发点A，则θ=已知m∈R，则“m＜10”是“lgm＜1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |